はじめに
北海道大学の吉田准教授の講義を12月3日に受講した。これに先立って、予習したけど、驚いたのはテキストの多さ。表紙を含めて106ページにわたる力作だ。これを10時25分から12時10分の105分にほぼ英語で駆け抜けた。スライド1枚で1分は標準的なペースだけど凄い。当日投影されたのはほぼ英語だけど、事前に配布された資料は日本語も残してあるので、個人的には理解が深まり、細かな配慮に感謝した。
脳型情報処理機械論#9
その1:講義前の予習(前回の投稿)
その2:自由エネルギー原理(⇨ 今回の投稿)
その3:知覚と行動選択・意識(次回の投稿)
自由エネルギー原理の提唱者
最初に自己紹介があったが、これは前回の投稿で説明したので割愛する。次に、自由エネルギー原理(Free-energy Principle)を提唱したカール・ジョン・フリストン(Karl John Friston)を紹介された。フリストンは、1959年7月12日生まれなので、現在62歳だ。英国のユニバーシティ・カレッジ・ロンドンの神経科学教授であり、脳イメージングの権威であり、「自由エネルギー原理と予測符号化理論」の主唱者だ。英語版のWikiにはその経歴や業績について次のような記述がある。
現在は、ユニバーシティ・カレッジ・ロンドンの神経科学教授です。 国立神経学・神経外科病院の名誉コンサルタントを務めています。統計的パラメトリックマッピング(SPM)を考案した。SPMは画像データを解析するための国際標準であり、一般線形モデルとランダムフィールド理論に基づいています。1994年には、ボクセルベースモルフォメトリー(BVM:voxel-based morphometry)を開発しました。BVMは、神経解剖学的な違いを検出するもので、臨床的にも遺伝子研究の代用としても使用されています。これらの技術的貢献は、統合失調症の研究と価値学習の理論的研究が動機となっています。1995年、この研究は統合失調症の切断仮説をChris Frithとの共著で発表しました。2003年には、脳のような分散システムのアーキテクチャを推論するために使用される動的因果モデル(DCM:dynamic causal modelling)を考案しました。数学的な貢献では、時系列分析のための変分ベイズ法である変分フィルタリングと動的期待値最大化(DEM:dynamic expectation maximisation)があります。フリストンは人間の脳における機能統合のモデルと、ニューロンの相互作用を支える原理を研究しています。フルストンの理論的神経生物学への貢献は、ベイズ脳における能動的推論である変分自由エネルギー原理(FEP:Free Energy Principle)です。2020年には、COVID-19パンデミックの政府公式諮問機関Scientific Advisory Group for Emergencies(SAGE)に代わる独立したSAGEのメンバーとなっています。1996年、フリストンは、Human Brain Mappingにおける最初のYoung Investigators Awardを受賞し、バイオ・メディカル科学への貢献が認められ、1999年にはAcademy of Medical SciencesのFellowに選出されました。2000年には、国際的なヒューマン・ブレイン・マッピング組織の会長に就任しました。2003年にはミネルバ・ゴールデン・ブレイン賞を受賞し、2006年には英国王立協会のフェローに選出され、2008年にはコレージュ・ド・フランス・メダルを受賞しました。2011年には、ヨーク大学から名誉博士号を授与され、生物学会のフェローとなりました(出典:Karl John Fristonより要約)。
参考文献の紹介
フリストンの紹介の後に自由エネルギー原理(FEP)に興味がある人のための図書が紹介された。図書館で調べると、「自由エネルギー原理入門」は貸し出し中だったので予約した。「脳の統一理論」を貸し出し可能だった。今度図書館に行ったら借りて読んでみようと思う。あらすじは次のようなものらしい。

(出典:講義資料より)
ワークショップの紹介
2021年12月13日と14日にオンラインで「脳における自由エネルギー原理の実験と検証」をテーマとするワークショップが開催される。チュートリアルの講師は我らが吉田准教授だ。日本語で行われると言うのも嬉しい。目的は「自由エネルギー原理(Free energy principle, FEP)」の基礎的な理解を深めることだ。講義の中ではRを用いた演習も予定している。Rの初心者でも利用できるようにRStudio Cloudを利用する。このイベントには実験研究者と理論研究者が一堂に会してFEPの生物学的メカニズムの進歩を共有する予定だ。自分もすぐに登録した。今から楽しみだ。

(出典:Free Energy Workshop)
本日の講義前提条件
ベイズ型脳仮説(Bayesian brain hypothesis)
私たちの知覚体験は、感覚入力をトップダウンで解釈するため、推論としての近くという概念が提唱されています。知覚は生成的な行為であり、知覚、認知、感情、社会文化的な期待をベースに感覚信号の原因に関する脳が最善の推測を行う。つまり、人は目に見えるものを認識しているのではなく、認識しているものを見たと認識すると言うことだ。
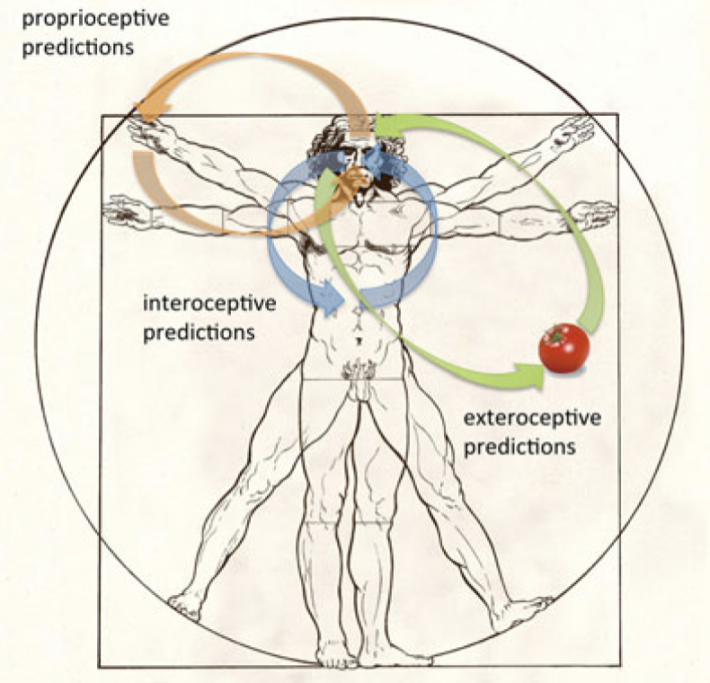
(出典:Cambridge Core)
エルンスト・マッハの感覚の分析
吉田准教授のお気に入りの絵がエルンスト・マッハの著書「感覚の分析」に収録された自我の視点のイラストだ。マッハが自分の左目で見るものを忠実に描こうとしている。右側は鼻、右下は口髭、上は瞼だ。自分の身体と周囲の世界を連続性を描いたものだ。極めて写実的だけど、実際にこのようには知覚しない。
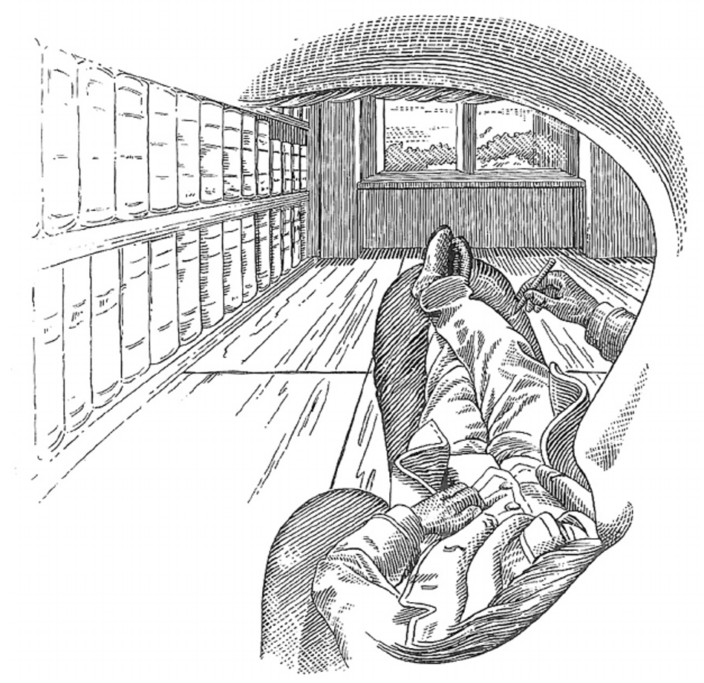
(出典:research gate)
高精細な中心窩(fovea)
カメラのレンズは中心も周辺も同じ解像度だ。しかし、人間の眼の解像度は中心部は非常に高精細になっている。この中心部分を中心窩(ちゅうしんか)と呼び、英語では”fovea”とか、”fovea centralis”と呼び、網膜の黄斑部の中心に位置している。読書したり、運転したり、スポーツしたりするときに、中心窩の高精細な中心視野が重要な機能を担っている。一方、中心窩の外縁は傍中心窩(parafovea)と呼び、さらに外側は周中心窩(perifovea)と呼ぶ。傍中心窩は中間の領域であり、神経節細胞層が5層以上の層を成す。周中心窩は網膜神経節細胞が層構造をなしている最も外側の領域である。その外側には大きな周辺視野があり、低解像度の視覚情報処理に寄与している。視神経は中心窩由来の神経線維をおよそ50%含み、それ以外の網膜領域からの神経線維をおよそ50%含む。つまり、視覚による情報の半分は親指幅の視野角1度に集中しているといえる。
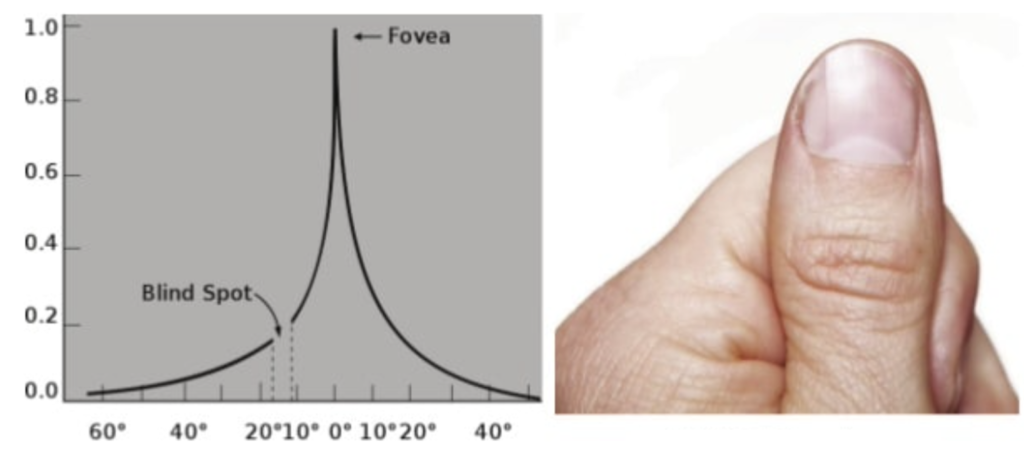
(出典:スライドシェア)
ベイズ推論
本日の講義を受ける上での基本的な知識の一つとしてベイズ型脳仮説について説明があった。テキストをそのままコピペするわけにもいかない。講義では数式を交えながら解説されたが、ここでは下の図のように「人間の脳は、階層的な予測符号化の原理に基づいて組織化されている。」という観点で説明する。組織化された脳は、本物のベイズ推論を効果的かつ効率的に行うことができると、現在の神経科学では推測している。多くの認知機能がベイズ推論に適しているため、このベイズ型脳仮説は認知科学にとって重要である。階層的な予測符号化は、ベイズ推論としてモデル化された認知の形態が脳内でどのように物理的に実装されるかを示している。しかし、この推測が本当に正しいかどうかについてはまだ審査中だ。
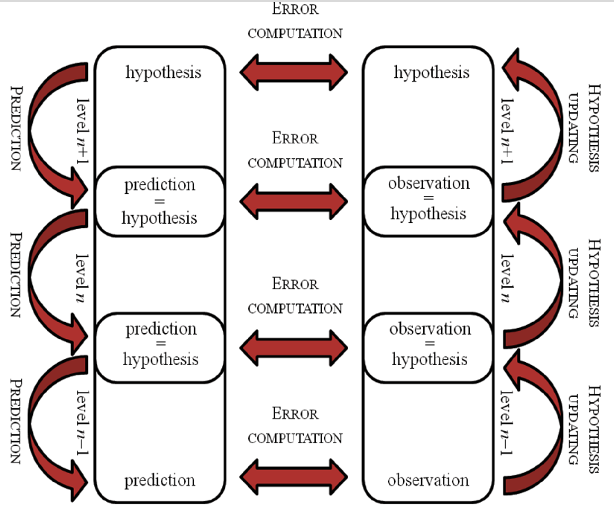
(出典:SEMANTIC SCHOLAR)
予測符号化
階層型予測符号化は、大脳皮質の組織化の有力なモデルである。このモデルでは、連続した階層レベルが、予測を伝える後ろ向きの接続と、予測エラーを伝える前向きの接続によって接続される。しかし、これまでの予測符号化モデルでは、神経伝達自体に時間がかかることをほとんど考慮されていなかった。つまり、動く物体のように時間的に変化する刺激の場合には、後方予測が新しい感覚入力とずれてしまう。前方と後方の両方の外挿機構を実装した拡張モデルを提示することで、予測誤差を最小化するために後方予測を再調整することも研究されている。
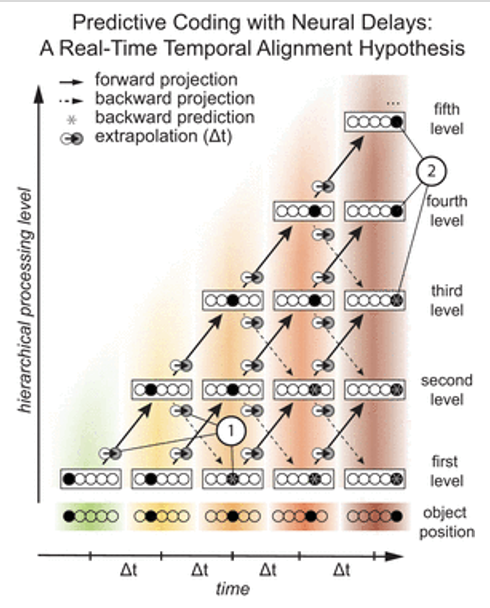
(出典:eneuro)
FEPに関するチュートリアル
能動的推論
ニューラルネットワークの概念的な考え方は、脳からヒントを得ている。人工ニューロンの複数の階層、接続を強化することによる学習と記憶などである。しかし、ニューラルネットワークで使用されているメカニズムは脳で観察される複雑さに比べると非常にシンプルだ。アクティブ推論は、教師なしの学習スキームであり、学習のために正しい答えやラベルを添付する必要はない。予測と感覚データの間の予測誤差により自主的に学習する。止まっている「動く歩道」に乗るときには、動いていないとわかっていても不思議な感覚を感じます。下の図(左)はJakob Hohwy氏の著書「予測する心(the predictive mind)」だ。こちらも一度は読んでみたい図書だ。
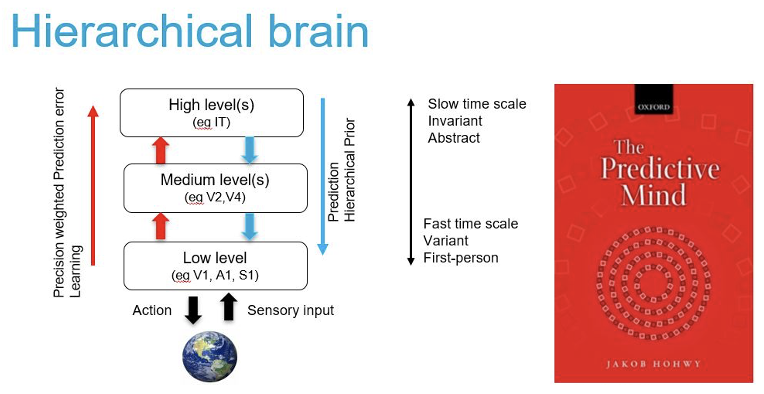
(出典:kaggle)
知覚(ベイジアンブレイン)
脳の働きをモデル化して、数式で記述すると下の図のようになる。この統一的な原理をまとめたのが自由エネルギー原理か。Aは、変分自由エネルギーを定義する量であり、Bは変文自由エネルギーの代替表現だ。Aは、システムをその内部状態である脳の状態μと、感覚入力s = g(η, a) + ωと、生物が環境をサンプリングする方法を変更する行動aに分割することを示す。外部環境は運動方程式η=f(η,a)+ωによって規定され、隠された世界の状態ηのダイナミクスを記述する。ωはランダムな揺らぎを示す。内部状態と活性状態の両方が相乗的に変化し、変分自由エネルギーを最小化する。この自由エネルギーは、感覚入力の関数であり、システムの内部状態によって符号化された隠れた環境原因の変分密度q(η:μ)である。Bの変分自由エネルギーの代替表現では、行動に関しては予測されたデータを選択的にサンプリングすることで自由エネルギーを抑える。逆に、内部状態の最適化により、変分密度は知覚、変分密度と真の事後密度の乖離を最小にする近似条件密度となる。この最適化により、変分自由エネルギーは驚きに対してより厳しい制限を課すことがでる。このようにシステムは感覚や生理的な状態が驚くようなことがないように世界に働きかけると言う。分かったような分からないような(笑)。
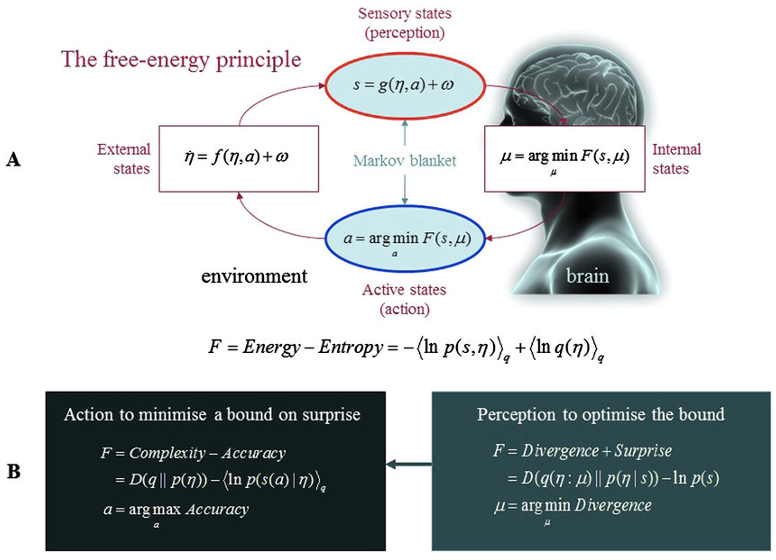
(出典:research gate)
まとめ
今回は、北海道大学の吉田准教授による脳型情報処理機械論の第9回目の講義についての投稿のその2として、講義の前半のパートについて、ネットで確認した情報を下に復習してみた。エントロピーは常に増大する方向に働くが、この自由エネルギーは最小化する方向に働くと理解した。つまり、脳は基本的にできるだけ消費エネルギーを少なくするように働くという原理だ。例えば、これは苫米地博士の得意なトピックだけど、「自宅の時計の様子をできるだけ詳細に描け」と言われてもなかなか思い出せない。毎日時計は見ているけど、それは時刻を知るためであって、時計の外観や模様や文字などは見ていても覚えていないものだ。脳は不要と認識したら視野に入っていても認知しないし、認知しないと音も聞こえない。このような事例は日常生活には溢れている。106ページのテキストの説明はまだまだ続く。
以上
最後まで読んで頂きありがとうございます。
拝
参考:その3で記載予定のトピック
・階層型予測符号化フレーム
・計算モデルに基づく視覚的特徴抽出
・KL距離(Divergence)
・能動知覚(Active vision)
・自由エネルギー(F)を最小化する3つの方法
・期待自由エネルギー
・変分自由エネルギーからアクティブ推論へ
・運動制御と感覚
・意識(consciousness)
・感情(emotion)




