はじめに
磯村博士の講義の概要については、すでに2回投稿したが、今回と次回で主なコンセプトやキーワードの解説を完了したい。
その1:生物脳における知能の数学的理論の概要(前々回の投稿)
その2:ニューラルネットワークの基本的事項(前回の投稿)
その3:変分ベイズの等価性の基本的事項(今回の投稿)
その4:自然淘汰から生まれる知性の基本的事項(次回の投稿)
キーコンセプトの解説
前回の投稿では、次の4つのコンセプトまでを記述した。今回はその続きを解説したい。
神経計算(Neural computation)
知覚的推論(Perceptual inference)
自由エネルギーの原理(Free-energy principle)
生成モデル(Generative model)
後方分布(Posterior distribution)
下の図の赤い線は事前(Prior)分布、緑の線は事後(Posterior)分布、および尤度関数(Likelihood)を用いたベイズ推論の例である。予測誤差は、事前の期待値と尤度関数のピークとの差(Prediction error)である。不確実性(Uncertainty)とは、事前分布の分散です。ノイズ(Noise)は、尤度関数の分散である。事後分布は、常に事前分布と尤度関数の間の妥協点である。
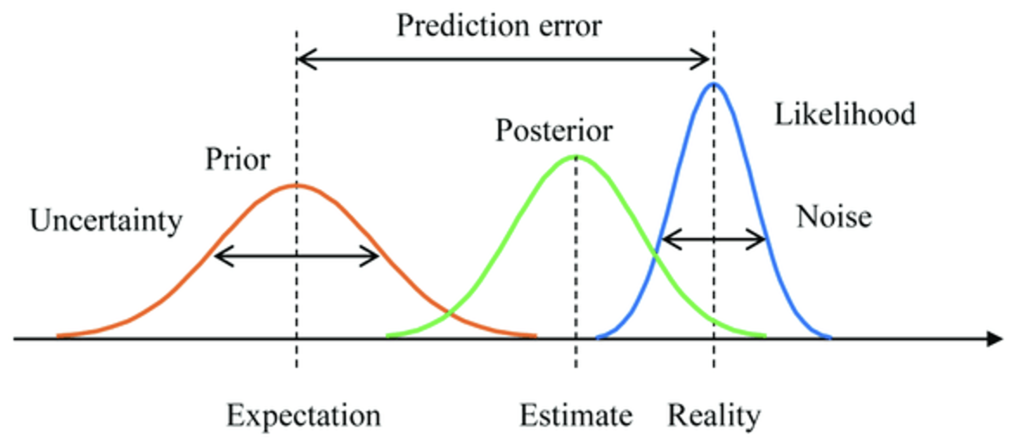
(出典:Research Gate)
変分自由エネルギー(variational free energy)
自由エネルギー原理。(A) 変分自由エネルギーを定義する量。これらの量は、システムをその内部状態であるμ(例えば脳の状態)と、環境との交換を記述する量、すなわち、感覚入力s = g(η, a) + ωと、生物が環境をサンプリングする方法を変更する行動aに分割することを反映しています。環境自体は運動方程式˙ η = f (η, a) + ωによって規定され、世界の(隠れた)状態ηのダイナミクスを記述します。ωはランダムな揺らぎを表します。内部状態と活性状態の両方が相乗的に変化し、変分自由エネルギーを最小化します。この自由エネルギーは、感覚入力の関数であり、システムの内部状態によってコード化された、隠れた環境原因の確率的表現(すなわち、変分密度)q(η : μ)である。(B): 変分自由エネルギーの代替表現で、その最小化が何を意味するかを示す。行動に関しては、感覚データの精度を上げる(予測されたデータを選択的にサンプリングする)ことでしか自由エネルギーを抑えることができない。逆に、内部状態の最適化により、表現(=変分密度)は、感覚入力の原因(=知覚)に対する近似条件付き密度となり、変分密度と真の事後密度の間の発散を最小化することができる。この最適化により、変分自由エネルギーは驚きに対してより厳しい制限を課すことができ、システムは感覚や生理的な状態が驚くようなことがないように世界に働きかけることができる。
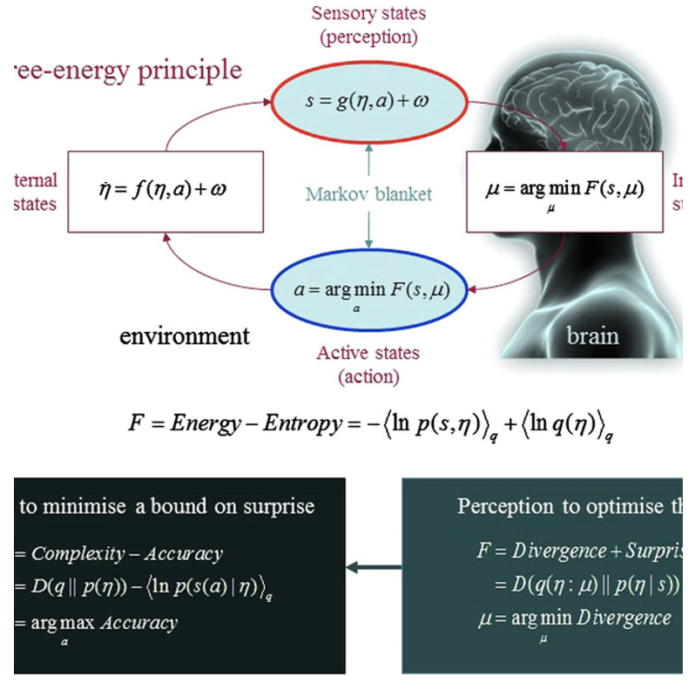
(出典:Research Gate)
スパイクコーディングレートモデル(Rate coding mode)
脳は発火率コードを使っているのか、それともスパイクタイミングコードを使っているのかという論争がある。この問題は、2つの観測値が刺激によって変化するかどうかを見る外部の観察者の視点に立っており、「どちらが神経活動において因果的な役割を果たしているか」という本質的な問題を見逃していると言える。下の図の(A)は、発火率の定義であり、時間平均としての発火率である。つまり、スパイク数nを観察時間Tで割ったものである。一方、下の図の(B)はN個のニューロンの空間平均としての発火率である。下の図の(C)は同一ニューロンのN回の試行の平均値としての発火確率である。
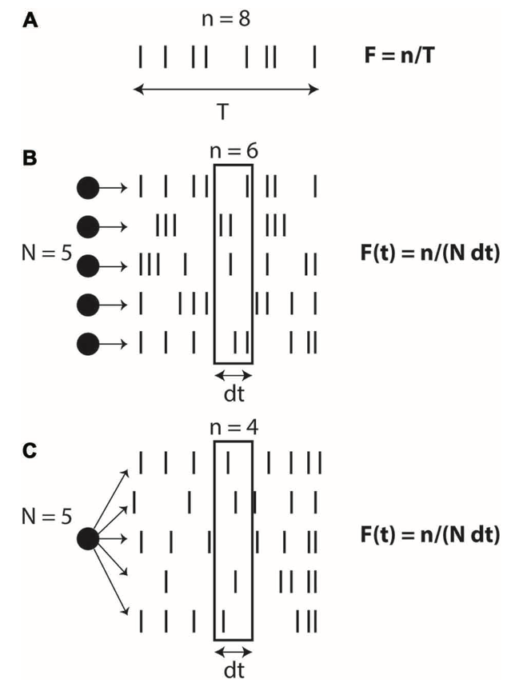
(出典:frontiers)
Hodgkin-Kuxleyモデルの方程式
ホジキン-ハクスリーモデル(Hodgkin-Huxley model)は神経細胞の活動電位がどのように発生し、伝播するかを記述する数学モデルである。神経細胞や心筋細胞などの興奮性細胞の電気的特性を近似した非線形微分方程式の集合体である。アラン・ホジキン(Sir Alan Lloyd Hodgkin, 1914年2月から1998年12月)はイギリスの生理学者・生物物理学者である。一方のアンドリュー・ハクスリー(Sir Andrew Fielding Huxley, 1917年11月から2012年5月)は、イギリスの生理学者・生物物理学者である。両名は、1952年にイカの巨大軸索(じくさく)における活動電位の発生と伝播の基礎となるイオン・メカニズムを説明するために、このモデルを記述した。この功績により、1963年にノーベル医学生理学賞を連名で受賞した。ホジキンさんとハクスレーさんが作ったこの数式モデル式は,65年経った今でも脳神経系の分野で非常に有効である。
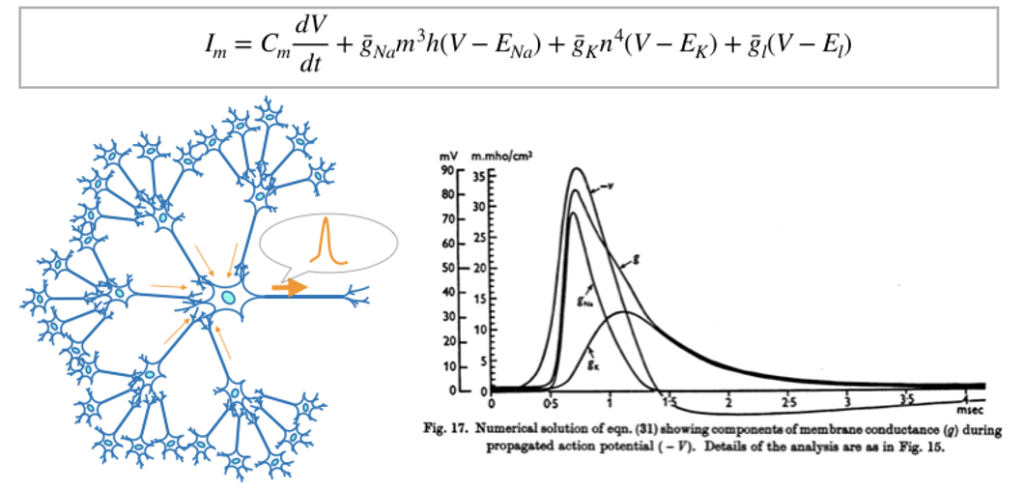
(出典:そうだ!研究しよう)
ヘッブ可塑性(Hebbian Plasticity)
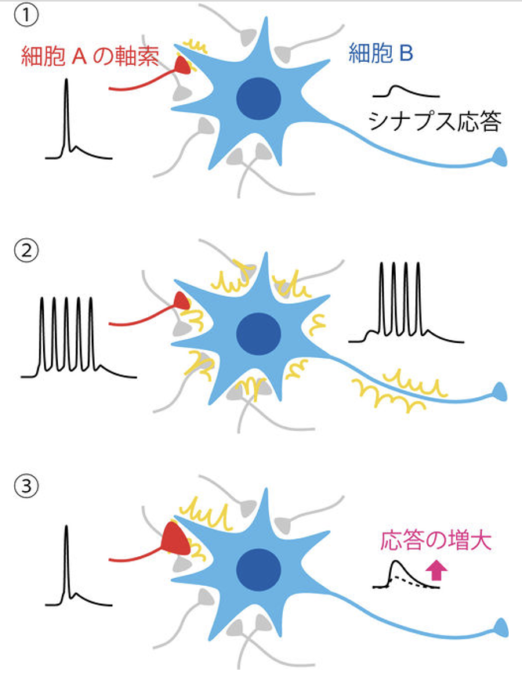
ヘッブ可塑性は、カナダの心理学者・神経心理学者ドナルド・オールディング・ヘッブ(Donald Olding Hebb、1904年7月から1985年8月)により、1949年に提唱された概念である。ヘッブはまず神経活動における「cell assembly(細胞集成体)」という概念を打ち立てた。ある受容器が刺激された場合には、それに応じて活動する細胞群によって細胞集成体が形成され、それはひとつの閉じた系として短時間活動できるようになると推測した。記憶とはそうした反響性活動の中で生じる永続的な細胞の構造変化であり、「ニューロンとニューロンの接合部であるシナプスというところに、長期的な変化が起こって信号の伝達効率が変化することが学習の仕組みである」という学習のシナプス仮説を著書『The Organization of Behavior』の中で唱えた仮説である。この仮説に基づくシナプス可塑性のルールは「ヘッブの法則」と呼ばれている。つまり、ヘッブの法則は、脳のシナプス可塑性についての法則である。下の図に示すように、ニューロン間の接合部であるシナプスにおいて、シナプス前ニューロンの繰り返し発火によってシナプス後ニューロンに発火が起こると、そのシナプスの伝達効率が増強される。また逆に、発火が長期間起こらないと、そのシナプスの伝達効率は減退する。著書の中では次のように記載している。
(“When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased.”)
つまり、「ニューロンAの発火がニューロンBを発火させると2つのニューロンの結合が強まる」となる。記憶とは適切なニューロン同士の結合力の変化である。ヘッブは神経活動における細胞集合体(cell assembly)という概念を提唱した。ある受容器が刺激された場合には、それに応じて活動する細胞群によって細胞集合体が形成され、それはひとつの閉じた系として短時間活動できるようになると推測した。記憶とはそうした反響性活動の中で生じる永続的な細胞の構造変化であり、「ニューロンとニューロンの接合部であるシナプスというところに、長期的な変化が起こって信号の伝達効率が変化することが学習の仕組みである」という学習のシナプス仮説を唱えた。
(出典:ヘブ則)
スパイクタイミングに依存した可塑性
下の図は、スパイクタイミング依存シナプス可塑性(STDP:Spike-Timing-Dependent Plasticity)を組み込んだニューロン回路である。ニューロン同士を結合するシナプス部では,入力されるスパイクと発火スパイクとの時間的関係でシナプス荷重が変化するSTDPと呼ばれる学習ルールが知られている。STDPにはスパイクの時間関係に対して対称的なものと非対称なものがよく知られています。
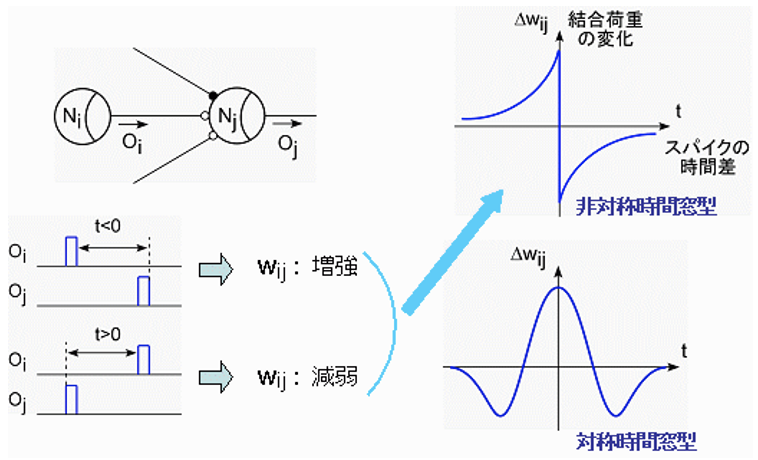
(出典:脳型集積システム研究室)
ニューラルネットワークによる変分ベイズ法
ベイズ理論をベースにしたベイジアンネットワークは、1980年頃に研究が始められた。これは統計・確率論的なアプローチによるAI技術である。ベイズ理論とは、観測を繰り返すごとに確率を修正して正解に近づけるという考え方であり、それをもとにしたベイジアンネットワークは因果関係を確率で表現するグラフィカルモデルである。ある事象に対する原因の確率と結果の確率をノードとし、それらをエッジで繋いだ形で表現される。観測によって得た新たな情報をベイジアンネットワークに投入するとそれぞれの確率が変化し、その確率に基づいて推論を行う。ベイジアンネットワークには原因から結果を推論することも、結果から原因を推論することも可能であるという特徴がある。ベイジアンネットワークはネットショップでのお勧め商品紹介、健康診断結果からの疑わしい病気の推定、スパムフィルタ、ウェブ侵入検知など、様々な分野での実用例がある。そして現在でも、ビッグデータ活用の手法の一つとして利用されている。統計・確率論的なAIに対しては、「統計と確率が基本にあるため、それは知性や知能ではない」という批判がある。膨大なデータの解析結果から単語の辞書的な意味を確率的に知ることはできるが、その単語の本当の意味を理解することはできない。人間の知能そのものを作るということを目的とした場合、統計・確率論的なAIはいつか限界に達すると予想される。その一方でニューラルネットワークの概念・手法も進化した。単純パーセプトロンの持つXOR問題は入力層と出力層の間に隠れ層を入れることで解決できることが判明している。
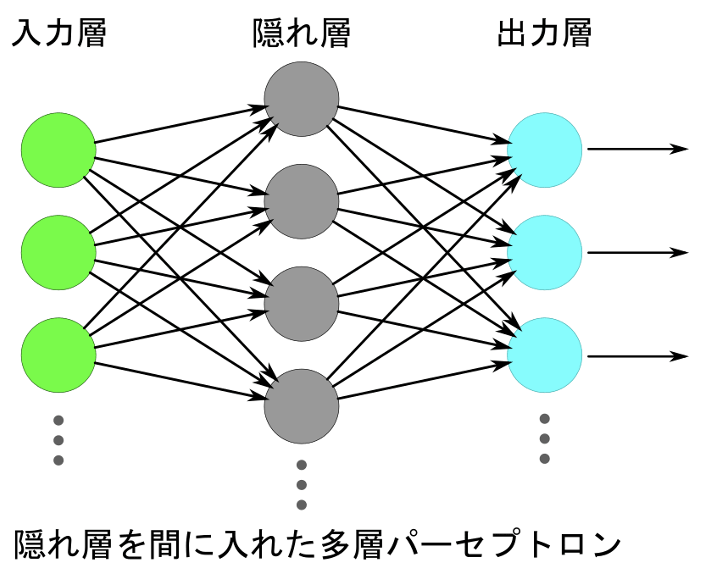
多層パーセプトロン
隠れ層を入れたものを多層パーセプトロン(Perceptron)と呼ぶ。パーセプトロンは、人工ニューロンやニューラルネットワークの一種である。米国の心理学者・計算機科学者フランク・ローゼンブラット(Frank Rosenblatt、1928年7月から1971年7月)が1957年に考案し、1958年に論文を発表した。このモデルは1958年に発表されたロジスティック回帰(Logistic regression)と等価である。ロジスティック回帰は、ベルヌーイ分布に従う変数の統計的回帰モデルの一種である。連結関数としてロジットを使用する一般化線形モデル(GLM) の一種でもある。1958年にデイヴィッド・コックスが発表した確率の回帰であり、統計学の分類に使われる。
(出典:スマイルエンジニアリングブログ)
まとめ
磯村博士の講義で聞いていてよく分からなかった用語などを一つずつ紐解いているが、調べれば調べるほど未知の用語が出てくる。しかし、この未知の用語と未知の用語の関連性が明確になり、点が線になり、線がメッシュになる程に理解度が深まり、分かった気になってくる。これが学習ということなのだろう。
以上
最後まで読んで頂きありがとうございます。
拝
次回は、自然淘汰から生まれる知性(Intelligence emerging from natural selection)の観点を中心に次のコンセプトについての解説にトライしたい。
インビトロネットワークの自由エネルギー原理
ミッシングコスト関数
二次曲線速度向上定理
実装可能性
ユニバーサルチューリングマシン
創発の定理
創発の定理の導出
生物学的知性と機械的知性




