はじめに
前回は第13回の講義のゲスト講師である土谷尚嗣教授の紹介やモナシュ大学での活動プロジェクトなどの紹介をした。今回は、講義の内容を理解する上で重要な6つのキーワードについて自分なりに深掘りしたいと思った。
その1:ゲスト講師の土谷教授はオープンマインド(前回)
その2:講義を理解するためのキーワード(⇨ 今回)
その3:序論・本論・今後の検討課題(次回)
キーワード
今回のキーワードはクオリアと統合情報理論(IIT)だ。これはともに第11回の大泉教授の講座で使われていたキーワードだ。アクセスは一般的な用語としては使っているが、今回の何か想いをこめて使っているように感じる。グローバルワークスペース論(GWT)なら以前投稿したが、GNWTは初めて聞く言葉だ。圏論(カテゴリー理論)と米田の補題(Lemma)は、米田教授の論文等で多用されているキーワードだ。これも講義では初めて聴く言葉だけど、非常に重要なコンセプトが含まれてるように感じる。
統合情報理論(IIT:Integrated Information Theory)
研究者の縁というものがあるのだろう。土谷教授は博士課程において脳科学のクリストフ・コッフ教授に師事されていて、クリストフ・コッフ教授はトノーニが提唱するIITを「意識についての唯一の真に有望な基礎理論」と称えている。数学的にはマトリックを用いた状態遷移により意識とは何かを数理的な仮説を証明する手法だ。
グローバル・ニューロン・ワークスペース理論(GNWT)
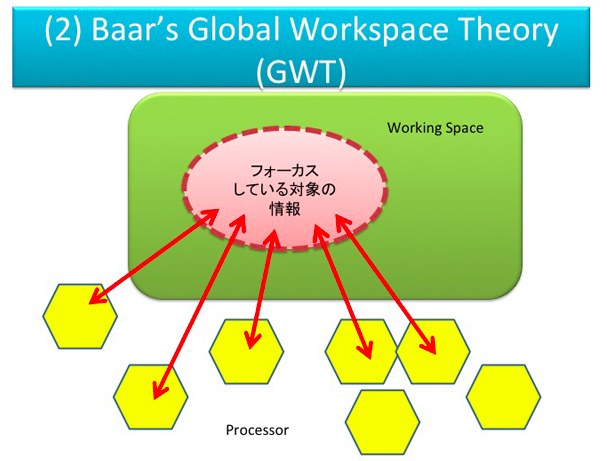
土谷教授に事前展開頂いた英文資料(Wk8)によると、GNWTとはグローバル・ニューロン・ワークスペース理論(Global Neuronal Workspace Theory)の略であり、意識に関する有力なモデルであると説明されている。米国カリフォルニア州サンディエゴの神経科学研究所のバーナード・J・バース(1946年生)が認知構造や意識に関するグローバルワークスペース理論(GWT:global workspace theory)を提唱されている。GNWTは、このGWTの理論をベースにして、さらに進化させた理論のように理解できる。人工知能には、シンボリズムとコネクショ二ズムという2つの流れがある。ディープラーニングなどのアルゴリズムは後者のコネクショニズムだ。一方、GWTは前者のシンボリズムだ(出典)。GWTは、下の図に示すように、多くのプロセッサーで処理した内容のうち意識が向いているものがワークスペースで処理されるというモデルのようだ。目に映っているものも意識していなければ認識していないことは日常発生するが、そのようなことを示しているのだと理解する。
グローバルワークスペース論(GWT:Global Workspace Theory)
Global Workspace Theoryです。情報が書き込まれるWorking Spaceといろいろなプロセッサ(小さな機能的知能)があって、プロセッサはWorking Spaceを処理する役割を持ちます。その中で、いま意識が向いている対象の情報をフォーカスして、いろいろな処理を書きます。フォーカスがずれると、プロセッサは新しくフォーカスされた情報にいって処理する。このモデルを「劇場モデル」といいます。認識する対象たちが舞台にあがっていて、舞台照明のフォーカスが当たっているところが意識なのだという考え方です。これは、黒板モデルと近い考え方ですが、より認知的な、意識的な描像になっています。みんな違う分野から似たようなことを言っているわけです(参考)。
(出典:mediagene)
クオリア(意識の内容)
今回の講義の中心的なコンセプトがこのクオリアであり、クオリアについては第13回の大泉教授の講義の後にも次のように投稿した。今回、土谷教授から展開頂いた資料には、狭義の定義と広義の定義が示されていた。狭義のクオリアはある一瞬の意識経験における何らかの場所や意識に登っている物体の一部から選び出した意識経験のある一側面だ。そして、広義の意味では、ある一瞬の意識経験の質全てを指す。特に、先に示した統合情報理論(IIT)が扱うクオリアは主に広義のクオリアだと考えて良いとあった。著名な作家や画家には高い映像記憶能力(Eidetic memory)を持つことが多い。小学生の時に路地から自転車で飛び出して、危うくタクシーに引かれそうになったことがあり、その時の映像は本当にスローモーションで、その時の運転手の顔の表情やタクシーのナンバーまで意識できていたように思う。AKB48を卒業した川栄李奈もこの映像記憶能力が高いと言われている。川栄は一般にはおバカキャラだけど、実は高い記憶力を持っていて、人の誕生日や電話番号など一度見れば記憶する。最近ではNHKの朝ドラのとと姉ちゃんや大河ドラマのいだてんや青天を衝けにも出演し、現在放映中のカムカムエヴリバディにもトリプル主演の一人を務める。話が脱線した、このクオリアに関する能力も人や状況によって大きく異なる傾向があると思う。
アクセス
今回の講義では、クオリアとアクセスをセットでスパーリング課題のところで使われていた。スパーリング課題とはボクシングの練習のことではない。これは、カリフォルニア大学アーバイン校の認知科学及び神経生物学・行動学の特別教授を務める米国の認知心理学者ジョージ・スパーリング(George Sperling、1934年生)が発案した課題だ。スパーリングは、「人間は視覚世界の完全なイメージを一瞬だけ記憶し、その後記憶から破棄される」という仮説を思いつき、その裏付けとなる実験をしたものをスパーリング課題と呼んでいる。具体的には、下のような図を一瞬画面に示し、それを生徒に答えさせる。自分はアルファベットのマトリックスと答えたけど、ネイティブの多くは「ZOSA」、「UIB」、「ZSOUBY..」、「ZOWY」、「C」などの回答があった。確かに12文字全ては記憶できない。この映像として捉えることをクオリアとし、個々の文字の認識に進むことをアクセスと呼んでいるようだ。文字をアクセスしようとすると、短い時間なので12文字を認識することはできない。しかし、川栄李奈のように高い映像記憶能力を有する人であれば、その映像記憶をたどって、全ての文字を思い出すことができるのかもしれない。映像として記憶する行為は無意識での行為であり、そこに書かれた文字を1文字ずつ認識しようとするのは意識的な行為だ。ドラゴン桜で、英語のリスニングでは、メモを取らないという指導があった。これは、メモを取るというアクセス行動をしている期間は、どうしてもヒアリングというクオリア的な行動が疎かとなり、結果的に全貌を理解できなくなるという解説だった。ただし、同時通訳者のように、聴きながら書くという能力を持つ人であれば、クオリアとアクセスを同時に行うことも可能なのかもしれない。

(出典:土谷教授からの事前展開資料)
圏論(カテゴリー理論)
英語では、Category theoryという。代数的位相幾何学やホモロジー代数に大きな業績を残したポーランド・ワルシャワ出身の数学者サミュエル・アイレンベルグ(Samuel Eilenberg, 1913年9月から1998年1月)と、アメリカの数学協会会長を1951年から1952年に勤めた数学者ソーンダース・マックレーン(Saunders Mac Lane, 1909年8月から2005年4月)が1942年から1945年にかけて「Categories for the Working Mathematician(圏論の基礎)」を発表している。この圏論と概念は、恥ずかしながら今回の講義で初めて知ったワードであるが、数学的には非常に重要な概念だ。数学的には、位相空間上の層のなす圏の概念をさらに一般化したのがトポス(topos)だ。ドイツ出身のユダヤ系フランス人の数学者であるアレクサンドル・グロタンディーク(Alexander Grothendieck、1928年3月から2014年11月)はヴェイユ予想(Weil conjectures)の解決に取り組み、ベルギーの数学者であるプリンストン高等研究所のピエール・ドリーニュ教授(Pierre Deligne、1944年10月生)が1974年に解決した。ピエールは、高等師範学校で数学を学び、26歳でフランス科学研究所(IHÉS)教授に就任し、34歳のとき数学のノーベル賞とも呼ばれるフィールズ賞を受賞している。ヴェイユ予想とは、数学者のアンドレ・ヴェイユが1949年に発表した非特異代数多様体上の合同ゼータ関数におけるリーマン予想の類似だ。このヴェイユ予想解決に向けた代数幾何学の変革の中で、数論的な図形上で有意義なホモトピー・コホモロジー的量が定義できる細かい「位相」を考えるために導入された。圏論は、このように欧州の偉大な数学者により研究が進められた概念だ。話が外れてしまうが、ポーランドが気になって、調べたことを下に示す。日本の縄文土器と瓜二つの縄目文土器がヨーロッパで発掘されていることは知っていたが、ポーランドがその中心地とは知らなかった。
米田の補題(Yoneda Lemma)
先の圏論における最も重要な結果が米田の補題だ。これは、日本の数学者米田信夫(1930年3月から1996年4月)が提唱したもので、小さなhom集合をもつ圏Cについて、共変hom関手hom(A, _):C→Setから集合値関手F:C→Setへの自然変換と、集合である対象F(A)の要素との間に一対一対応が存在するという定理である。米田信夫は1961年に東京大学で理学博士号を取得したが、その時の博士論文の題は「On ext and exact sequences」だ。日本語に訳するとどうなるのだろう。圏論を理解するには、関手(functor)や、射などの理解も求められる。なお、補題とは補助定理(helping theorem)のことであり、その補助定理自体が興味深いと言うよりも、より大きな結果を得る一歩として使われる証明された命題である。圏論のための補題ということになる。また、寄り道になるけど、コラッツの問題も興味深いので少し記載しておく。
まとめ
講義の内容を理解するために重要と思われるキーワードを少し掘り下げて理解しようとした。キーワード自体よりもその周辺も興味深かった。これまで、多くのコンセプトには欧州の科学者の名前が数多く登場するが、日本人で独創的なコンセプトを提示した人はいなかったのだろうかと少し残念な気持ちがあったが、今回米田信夫という数学者がYoneda Lemmaとして圏論に発展に寄与していることを知り、少し誇らしい気持ちになった。同時に、ポーランドからは優秀な科学者や数学者が数多く輩出していたが、その多くが第二次世界大戦で大量虐殺されていることもショックだ。同時に、そのポーランドには日本の縄文土器とそっくりな縄目文土器が発掘された場所であることも不思議な感じだ。ポーランドやトルコにはまだ旅行したことがないが、コロナ禍が沈静化したらぜひ足を伸ばしたいと思った。
以上
最後まで読んで頂きありがとうございました。
拝



