はじめに
磯村博士の講義の概要については、前回に投稿した。2つの疑問に対する見解のまとめのみを投稿したが、これだけで理解できる人は凄いと思う。恥ずかしながら自分は理解できない用語やコンセプトが多すぎて訳がわからない。そのため、関連するキーワードを一つずつ調べて自分なりに理解した範疇で解説したい。
その1:生物脳における知能の数学的理論の概要(初回の投稿)
その2:ニューラルネットワークの基本的事項(今回の投稿)
その3:バリアブルベイズの等価性の基本的事項(次回の投稿)
その4:自然淘汰から生まれる知性の基本的事項(次々回の投稿)
磯村博士の研究内容
今回の講義を理解する上で、講師である磯村博士がどのような研究をしてきたかをレビューすることは理解を深める近道だと思う。その意味で3つの研究論文と1冊の著書を紹介しておきたい。
研究論文1:Bayesian Filtering with Multiple Internal Models: Toward a Theory of Social Intelligence
英語のタイトルを見てもなんだかよくわからない。日本語にすると、「複数の内部モデルによるベイズ・フィルタリング。社会的知性の理論に向けて。」というところか。概要も英語だけど、日本語に意訳すると次のような感じだろう。キーワードは「ベイズ」と感じる。ベイズの定理については、5回目の講義メモでも解説したが、重要な概念だと再認識される。
動物が社会的知性を発揮するためには、誰とコミュニケーションをとっているかを認識する必要がある。この推論を行う1つの方法は、遭遇する可能性のある各同種生物の内部生成モデルの中から選択することである。しかし、これらのモデルは、何らかの形でベイズの信念更新(Bayesian belief updating)によって学習されなければならない。これは興味深い問題を引き起こす。つまり、特定の同種生物が生成した感覚入力を受け取ったとき、動物はどの内部モデルを更新すべきかをどのように知るのだろうか?本研究では、理論的かつ神経生物学的に妥当な解決策として、複数の生成モデルの下で、聞くことや理解するといった感覚入力を生成するプロセスや、話すことや歌うことといったそれらの入力を再現するプロセスの推論と学習を可能にする方法を検討する。これは、最近の理論神経生物学の進歩、すなわち能動的な推論と事後(post hoc)のオンラインなベイズモデル選択に基く。つまり、この方式では、感覚入力をそれぞれの生成モデルに当てはめる。モデルのパラメータは、モデルの証拠として各モデルが入力を生成した可能性に比例して更新される。提案された方式は、本物のゼブラフィンチ(zebra finch)の鳥の鳴き声を使って実証される。この方式は、鳥の鳴き声生成の生理学的に妥当なモデルを用いて実装されている。一般化ベイズフィルタリングとモデル選択を組み合わせることで、それぞれが異なるパラメータを持つ生成モデル間での学習が成功することを示している。これらの結果は、複数の感覚情報が存在する社会環境で推論を行う際に、複数の内部モデルを持つことの有用性を示している。(出典:NLM)
著書:NEURAL COMPUTATION
2019年12月1日に出版された図書だ。タイトルのNeural Computationを日本語にすると神経計算だ。この辺りから主要なコンセプトを紐解く必要がありそうだ。著者は「磯村博士と、University College London(UCL)のThomas Parr氏とKarl Friston氏の3名での共著となっている。表紙にあるのは先の論文にあったゼブラフィンチのように見える。

(出典:MIT Press)
研究論文2:Multi-context blind source separation by error-gated Hebbian rule
日本語にすると「誤差を考慮したヘブン・ルールによるマルチコンテキスト・ブラインド・ソース・セパレーション」だろうか。この論文も英語だけど、概要を日本語にすると次のような記述だった。ここでのキーワードはBSSとEGHRと理解する。
動物は,自分が置かれている状況に応じて推論を調整する必要がある。これは、マルチコンテクスト・ブラインド・ソース・セパレーション(BSS:blind source separation)タスクに必要なことで、エージェントはコンテクストに依存した混合物から隠れたソースを推論する必要がある。エージェントは、すべてのコンテキストに対して、この混合プロセスを反転させることが期待される。十分に冗長な感覚入力を用いて、エラーゲーテッド・ヘッブの法則(EGHR:error-gated Hebbian rule)を実装したニューラルネットワークが、このタスクをうまく学習できることを示す。このネットワークは、学習後、経験したすべてのコンテキストの記憶を保持することで、シナプスを更新することなくマルチコンテキストBSSを実行することができる。これは、コンテクスト間で低次元のソースを抽出することによる次元削減のためのEGHRの魅力的な利用法を示している。最後に、もしコンテクスト間で共有される共通の特徴があれば、EGHRはそれを抽出して、経験のないコンテクストにもタスクを一般化することができる。この結果は、動物における知覚適応のモデルとしてのEGHRの有用性を強調するものである。
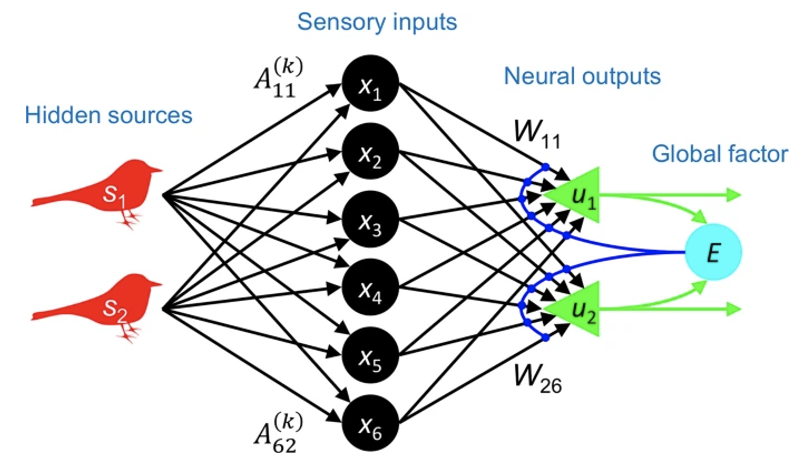
(出典:scientific reports)
研究論文3:In vitro neural networks minimise variational free energy
これは、2018年5月に投稿された論文で日本語で言えば「変分自由エネルギーを最小化する体外式ニューラルネットワーク」だろうか。この論文の概要も英語なので日本語にすると次のような感じだろうか。ここでは、自由エネルギー原理に加えて、対比関係で使われているin vitro反応とは生体外培養の意味で、in silico反応はシミュレーションしたという意味だった。
本研究では、ベイジアンの観点からニューロン・エンコーディング問題を扱う。具体的には試験管内のニューロンネットワークにおけるニューロンの応答が、自由エネルギー原理の下での理想的なベイズ観察者の応答と一致するかどうかを問う。簡単に言えば我々はin vitroの皮質細胞培養に既知の統計的構造を持つ刺激列を与えた。次に、記録された神経細胞の反応が、自由エネルギー最小化に基づく信念伝播(belief propagation)の変分メッセージパッシング(variational message passing)と一致するかどうかを尋ねた。自由エネルギーの最小化(証拠の最大化)に基づく変分メッセージパッシング(信念の伝播)と一致するかどうかを調べた。実際には、2つの問題を解決する必要があった。1つ目は、感覚刺激の原因またはソースのベイズ最適エンコーディング(Bayes-optimal encoding)を定式化することである。次に、これらの理想化された反応が、観察された電気生理学的反応を説明できることを示すことである。電気生理学的な反応を説明できることを示さなければならない。本研究では、理想的なベイズ神経コード(the ideal Bayesian neural code)である最適なニューラルネットワークのシミュレーションを行い、理想化されたin silico反応と記録されたin vitro反応との対応関係を考察した。我々の目的は、自由エネルギー最小化によるin silicoの学習を再現するin vitroの神経ネットワークにおいて、機能的な特殊化と分離の証拠を見つけることであった。最後に、in vitroとin silicoの結果を組み合わせて、学習を精度と複雑さの変分情報平面上の軌道という観点から特徴づけた。
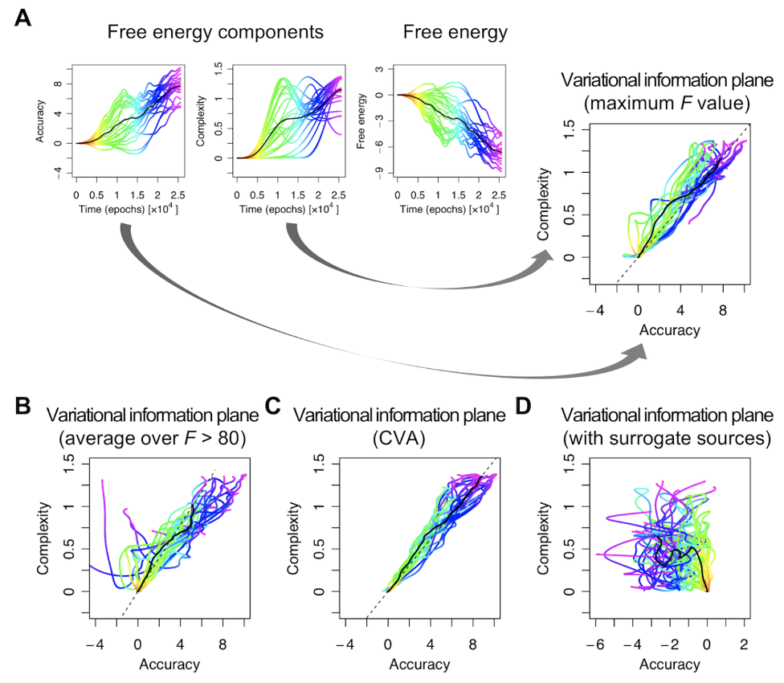
(出典:ReseachGate)
ペンタトニックスケールの威力(power of the pentatonic scale)
講義が始まるとYouTubeの動画が投影された。アメリカのジャズ歌手ボビー・マクファーリンこと、ロバート・キース・マクフェリン・ジュニア(Robert Keith McFerrin Jr.、1950年3月11日生まれ)の一風変わった演奏だ。これは、アル・ジャロウと並ぶ器楽的唱法を特徴とする。歌声に変化を加える方法として、歌いながら胸や頬を叩くなどの技巧も用いる。授業ではうまく音声が再生できなかったが、YouTubeで確認できる。00:43あたりでパフォーマーが初めての場所に立った時に聴衆が場所と声の高さを予測して皆同じ高さの声を出しているところが見どころだ。空間と音程を紐づけて聴衆が音を予測する能力を示す例として磯村博士のお気に入りだ。確かに面白いし、驚きでさえある。
キーコンセプトの解説
ここでは、先の磯村博士の論文で使われている重要な概念を含めて、ニューラルネットワークとバリアブルベイズの等価性の観点からいくつかのキーコンセプトの解説にトライしたい。
神経計算(Neural computation)
新しい概念を調べる時にWikiは便利だけど、これだと差別化できない。個人的には日本語のWikiで基本的な点を理解した上で、英語版やドイツ語版など他の言語のWikiを見ることが多い。言語によって書かれている内容の幅や深さが異なることが多い。ここでは神経計算の英語版を翻訳したものは次のようになる。かなり分かりやすい。計算論も3つに大別されるというのも面白いと思った。
知覚的推論(Perceptual inference)
講義では、野菜に見える絵を上下反転すると人の顔に見える絵を紹介してもらった。これは初めて見た。知覚的推論とは、過去の経験に基づいて構築された内部の神経表現から生じる予測から、感覚刺激を推論する能力のことである。ひらたく言えば、思い込みによる勘違いと言える。ベイズ統計的推論や決定論の手法は、行動を導く際にエラー・センシングを用いたり、感覚情報を予測する「生成」モデルを用いたりすることで、認知を適切にモデル化する。この枠組みでは、知覚は、感覚とは質的に異なるプロセスであり、感覚のフィードバックによって導かれる。蓄積された表現は、感覚刺激の内部モデルとして利用され、例えばオペラント条件付けのような長期的な関連付けを可能にする。知覚的推論の証拠として、物体知覚と物体記憶の皮質での共起、刺激の変化に対する一部のニューロンの反応の不変性、知覚が感覚から切り離される状況などの現象が挙げられる。知覚推論の文脈では、プライミング信号によって促進された大脳皮質の感覚領域は、感覚運動系の中でよく知られている運動反射と同様に、閉じたフィードバックループの中の比較対象とみなすことができる。成人の大脳皮質は、感覚フィードバックを用いて内部モデルを修正し、過去の経験に基づいて外界の予測を行うサーボ機構に似ていると考えられる。下の図(左)を見ると白い正方形があるとしか見えない。下の図(右)は白い三角形があるとしか見えない。これは面白い。
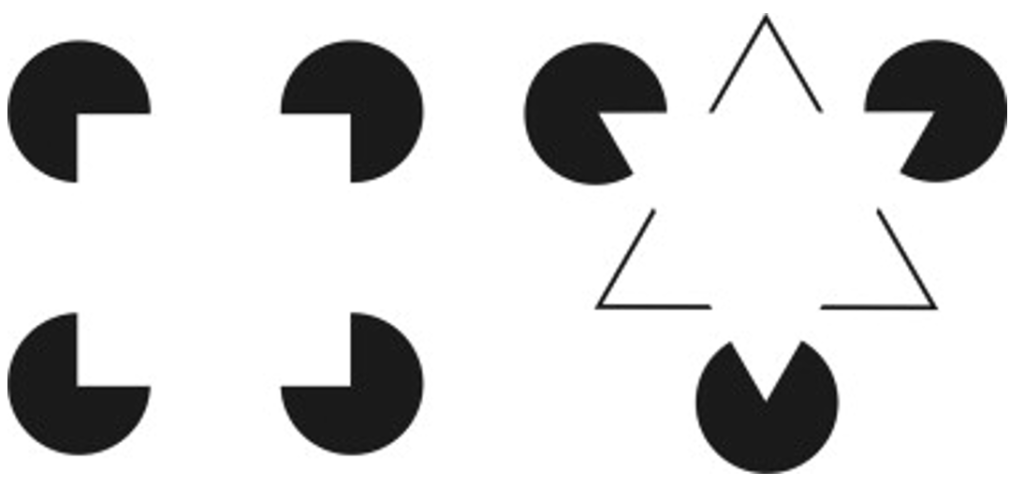
(出典:Science Direct)
自由エネルギーの原理(Free-energy principle)
英国ユニバーシティ・カレッジ・ロンドンの神経科学者であるカール・ジョン・フリストン(1959年7月生)やニューカッスル大学のマイケル・ブレイクスピア教授(Breakspear M)らによる「Perception and self-organized instability」では、自由エネルギー原理を「いかなる自己組織化されたシステムでも、環境内で平衡状態であり続けるためには、そのシステムの自由エネルギーを最小化しなくてはならない」と定義している。自由エネルギー原理とは、認識や行動についての適応理論であり、環境に対する予測可能性を上げるという原理によって、認識だけでなく行動も生成されるとする仮説に従った脳の理論である。自由エネルギー原理では、運動とは「目標となる状態の自己受容感覚を予測信号とし、それが達成されるように反射弓を駆動させる」こととされている。運動野から筋肉に伝えられるのは運動指令信号ではなく、目標となる姿勢の自己受容感覚であり、自己受容の予測である。
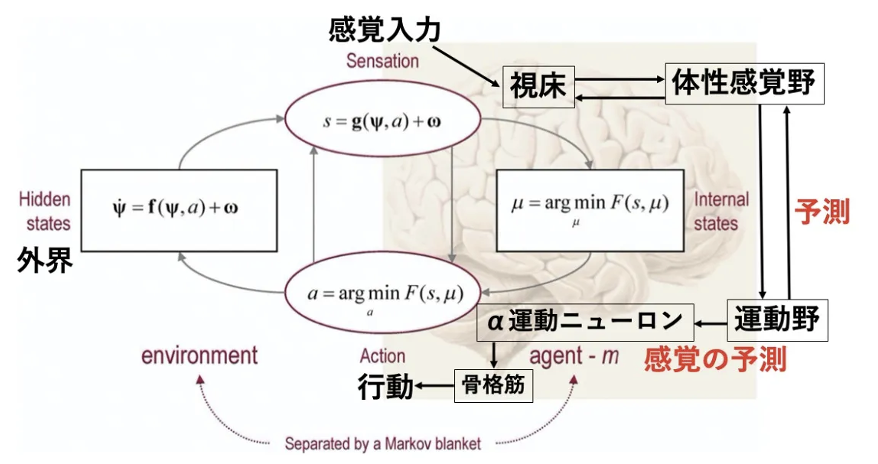
(出典:Graine)
生成モデル(Generative model)
生成モデルとして、下の図では、敵対的生成ネットワーク(GAN:Generative adversarial networks)、可変オートエンコーダー(VAE:Variational autoEncoders)、フローベースの生成モデルを示す。GANは、機械学習分野の研究者であるイアン・J・グッドフェロー(Ian J. Goodfellow)らが2014年に発表した教師なし学習で使用される人工知能アルゴリズムの一種である。GANは教師なしの学習問題であるデータ生成を、教師ありの問題としてモデル化する賢い方法を提供する。VAEは機械学習において、Googleの研究者であるDiederik P Kingmaとアムステルダム大学で機械学習を研究しているオランダのコンピュータ科学者マックス・ウェリング(1968年生)によって導入された人工ニューラルネットワークのアーキテクチャであり、確率的グラフィカルモデルと変分ベイズ法のファミリーに属します。最後のフローベースの生成モデルは、反転可能な変換のシーケンスによって構築される。他の2つのモデルと異なり、このモデルはデータの分布p(x)を明示的に学習しているので、損失関数は単純に負の対数尤度となる。
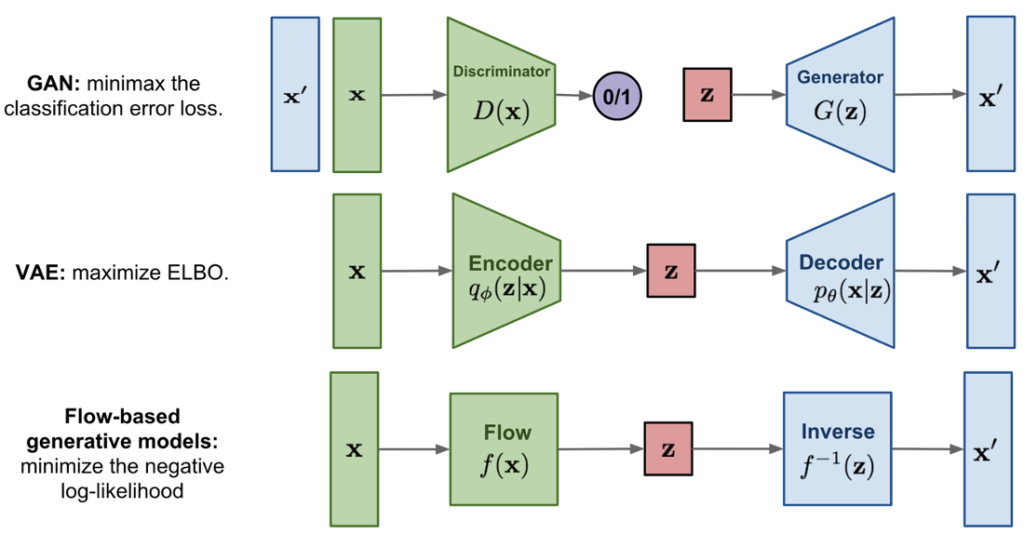
(出典:Lil`Log)
まとめ
磯村博士の研究論文や講義で疑問に感じたキーワード等の解説を試みているが、量的に多くなってきた。何が分からないかは分かってきた。これまで多くの科学者が頑張って研究してきた成果の上に現代の社会が成り立っていることを改めて感じる。また、研究者もだんだん現役の人になってきたのがなんとなく嬉しい。
以上
最後まで読んで頂きありがとうございます。
拝
(参考)
その3で解説するキーワード
後方分布(Posterior distribution)
可変自由エネルギー(variational free energy)
スパイクコーディングレートモデル(Rate coding mode)
Hodgkin-Kuxleyモデルの方程式
ヘッブ可塑性(Hebbian Plasticity)
スパイクタイミングに依存した可塑性
神経回路による変分ベイズ法
生体外培養神経回路の自由エネルギー原理
その4で解説するキーワード
ミッシングコスト関数
二次曲線速度向上定理
実装可能性
創発の定理
創発の定理の導出
生物学的知性と機械的知性




