- 1 はじめに
- 2 講師
- 3 今回のテーマ
- 4 4つの論点
- 5 前提となる知識
- 5.1 自己組織化:SO(self-organization)
- 5.2 制約条件付き自己組織化(SOC:self-organization with constraints)
- 5.3 大脳皮質機能分化の数理的モデル(Mathematical modeling of cortical functional differentiations)
- 5.4 非ホロノミック(nonholonomic)
- 5.5 バコノミック力学(Vakonomic Mechanics)
- 5.6 ラグランジュ・マルチプライヤー(Lagrange multipliers)
- 5.7 ニュートン力学(Newtonian Mechanics)
- 5.8 最適制御理論(Optimal Control Theory)
- 5.9 ディラック・ブラケット(Dirac Bracket)
- 5.10 Schrödinger方程式(Schrödinger equations)
- 6 まとめ
はじめに
10月29日(金)は、脳型情報処理基幹論第4回講義だった。講師は日本人だけど、資料はほぼ英語で、講義もほぼ英語、しかも内容が難解だった。と言うか、何が分からないかが分からないレベルだった(汗)。なお、この投稿は授業の講義メモではなく、講義で理解したことを分かりやすく解説するのが主旨だ。講義の内容が広範囲なので、複数回に分けてトライしたい。
その1:4つの論点と前提となる知識 (⇨ 今回の投稿)
その2:4つの論点(前半)のレビュー(次回)
その3:4つの論点(後半)のレビュー(次々回)
講師
今回の講師は、中部大学創発学術院の津田一郎教授だ。AI数理データサイエンスセンター(Center for Mathematical Science and Artificial Intelligence)も兼任されている。著書を見ると、下の図(左)は翻訳本であり、下の図(中)は数学に関する著書で、下の図(右)が津田さんだ。カオスや複雑系と呼ばれる分野を専門とされていて、最近では数学で脳の情報処理の仕組みを解き明かす複雑系カオス脳理論に取り組んでおられ、その最前線の内容を披露頂いた。また、講義自体は、ZOOMによるオンライン授業であり、対面と違って生の雰囲気が味わえないのと、名刺交換ができないのが残念だった。

(出典:WiKi)
今回のテーマ
講義のガイダンスでは、「制約と機能分化による自己組織化」であったが、これだけではよく分からない。配布された資料のタイトルでは、「科学的アプローチと科学への貢献(A Dynamic principle of functional differentiaion)」とあった。表紙を捲ると「(カオスな動的システム+脳科学)n乗(n>1)」とあった。津田先生は数学が大好きなようだ。なお、下の図は、資料の表紙に絵柄に似た図をネットで見つけたものだ。これは、オランダの画家マウリッツ・コルネリス・エッシャー(1898年6月から1972年3月)の作品で、だまし絵(トロンプ・ルイユ)や、数学的な絵画が得意のようだ。

(出典:メタモルフェーゼ)
4つの論点
今回は前述の通り複雑系カオス脳理論の分野の専門家である津田教授から、次の4つの論点について解説頂いた。約90分の講義を受けたが、正直消化不良で、これが答えというものをコンパクトに記載するのが現在の自分には難しいが、徐々に紐解いていきたいと思う。
論点1:ニューロンはどのように生成されたか?
How were neurons generated?
論点2:機能モジュールはどのように生成されたのか?
How were functional modules generated?
論点3:神経細胞はどのようにして機能特異性を獲得したのか?
How did neurons acquire functional specificity?
論点4: 記憶システムの進化
Additional comments:Evolution of memory systems
前提となる知識
自己組織化:SO(self-organization)
自己組織化(SO:Self-organization)とは、自律的な振る舞いの結果として、秩序を持つ構造を作り出す現象という。英語版のWikiはもう少し詳しく次のように解説してくれている。

(出典:Self-Organization)
制約条件付き自己組織化(SOC:self-organization with constraints)
制約条件付きの自己組織化(SOC:self-organization with constraints)と自己組織化(SO)は何が違うかというと、制約条件があるかどうかだ。SOはマクロ的な秩序であり、ミクロなレベルでの分子や原子の相互作用によって生成されるが、SOCはシステムに作用する制約条件を介して生成されるという考え方だ。例えば、脳の機能文化はSOの典型例であるが、制約条件が全くないわけではない。一定の制約条件のもとで自己組織化の枠組みが定式化されるべきという考え方だ。これは数学的であり、機能的な要素は、システム全体に作用する制約条件のもとで自己組織化する。
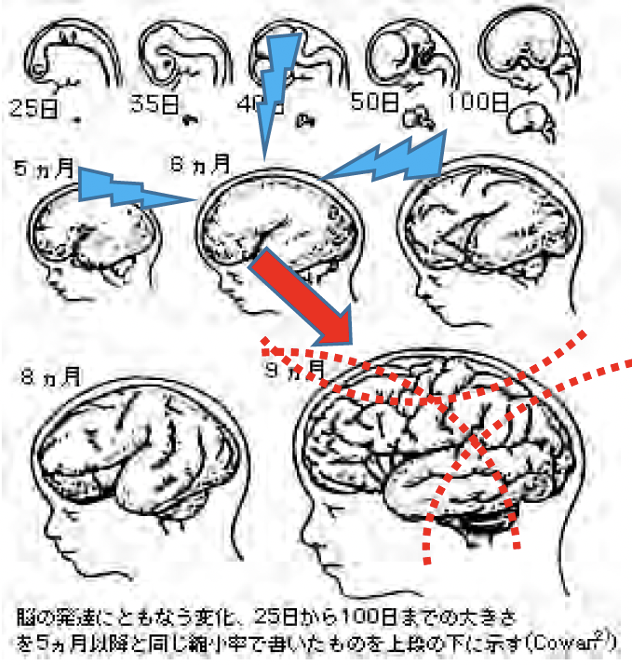
(出典:京都大学)
大脳皮質機能分化の数理的モデル(Mathematical modeling of cortical functional differentiations)
大脳皮質に関しては、第1回講義でも投稿したように、下の図のような構造で、機能が局在化している。津田教授のすごいのは、この大脳皮質の機能の数学的モデルを考えるところだ。カールトンカレッジで数学の学士号を取得し、ミネソタ大学で生物統計学の博士号を取得したJack Pattee博士(参考)は次のように、動的制約と意図的制約があると考えている。動的制約がf(x,λ)であり、意図的制約がC(y)だ。
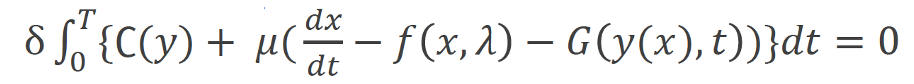
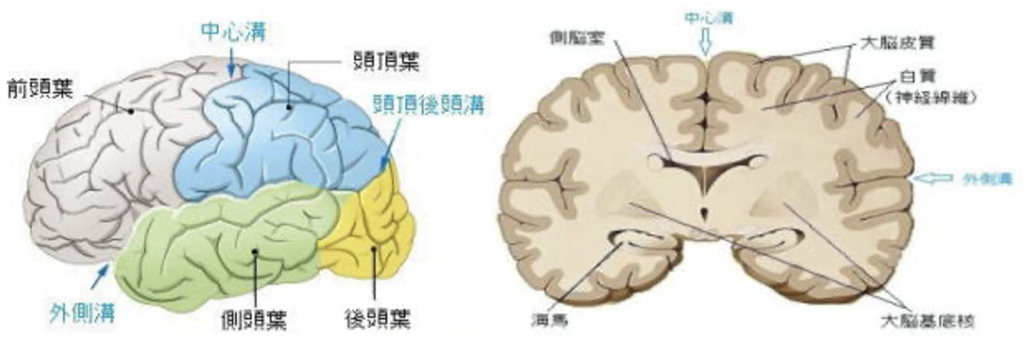
(出典:大脳皮質)
非ホロノミック(nonholonomic)
非ホロノミック(nonholonomic)とは、系の拘束条件の性質を述べた用語であり、力学系の拘束条件が可積分でないこと、ドリフトがあること、入力の数よりも多くの座標を制御できるといった力学系の拘束条件だ。拘束条件は、一般に系の座標(位置とか角度)と時間、座標の時間微分(速度や加速度)で表現される。なお、ホロノミック(holonomic)とは、この拘束条件が座標と時間のみで記述されるものだ。
(出典:東京大学)
バコノミック力学(Vakonomic Mechanics)
バコノミック力学(Vakanomic Mechanics)は系の挙動がLagrange乗数の未来値に依存することを許した体系である。非ホロノミックな拘束を扱う拘束系の解析力学はバコノミック力学と非ホロノミック力学に大別される。非ホロノミック力学が物理学的な因果律を保つのに対して、バコノミック力学は系の挙動がLagrange乗数の未来値に依存することを許した体系で゙ある。つまり、古典的な変分法の延長線上に存在してシステム理論的な動機をもつと言える。
ラグランジュ・マルチプライヤー(Lagrange multipliers)
ラグランジュの未定乗数法(method of Lagrange multiplier)とは、束縛条件のもとで最適化を行うための数学的な方法である。数学的最適化において、ラグランジュ乗数法は、変数の値を選択することで、1つ以上の方程式が正確に満たされるという条件等式制約の下で、関数の局所的な最大値と最小値を見つけるための戦略と言える。基本的な考え方は、制約のある問題を、制約のない問題の微分テストがそのまま適用できるような形に変換するだ。関数の勾配と制約条件の勾配の関係から、ラグランジュ関数と呼ばれる元の問題の再定式化を行う。ラグランジュ乗数法はKarush-Kuhn-Tucker条件によって一般化されている。いくつかの変数に対して、いくつかの関数の値を固定するという束縛条件のもとで、別のある1つの関数の極値を求めるという問題を考える。各束縛条件に対して未定乗数を用意し、これらを係数とする線形結合を新しい関数として考えることで、束縛問題を普通の極値問題として解くことができる。
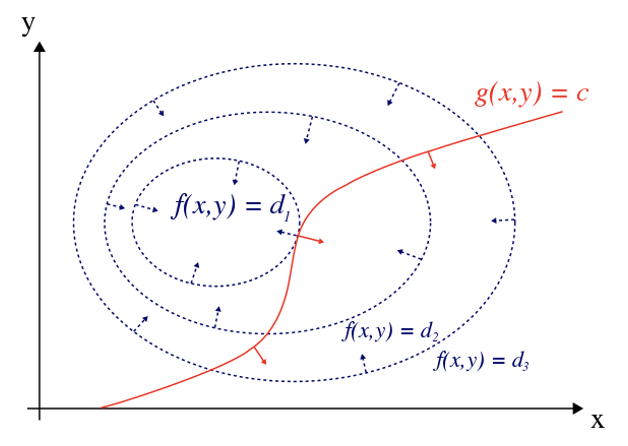
(出典:Lagrange_multiplier)
ニュートン力学(Newtonian Mechanics)
量子力学が出現する以前のニュートン力学や相対論的力学を古典力学と呼ぶ。特に、ニュートン力学(Newtonian Mechanics)は、投射物や巨視的な物体、宇宙船、惑星、星、銀河などの天体の運動を記述する物理理論である。英国の数学者、物理学者、天文学者、神学者、自然哲学者であるアイザック・ニュートン(1642年12月から1727年3月)が発見した物理的概念を彼に続く研究者により記述された数学的手法だ。なお、ニュートンがケンブリッジ大学の学生だったときには、1665年から1666年にかけてペストの大流行のために故郷のウールスソープへと戻り、故郷での休暇中に、いわゆる微分積分学、プリズムによる光学、そして万有引力の着想といったニュートンの三大業績が全て故郷に戻っていた25歳ごろの功績というのも有名だ。
(出典:Classical_mechanics)
最適制御理論(Optimal Control Theory)
最適制御(optimal control)理論とは、とは,与えられたシステムに対して,ある最適基準を達成するような制御則を求めるための理論である。目的関数が最適化されるような制御を見つけることを目的とする数理最適化である。制御問題には,状態変数と制御変数の関数であるコスト関数が含まれる。この場合の最適制御は,コスト関数を最小化する制御変数の経路を記述する微分方程式の集合となる。最適制御の理論はオートメーション工学ならびに応用数学の一部でもある。
ディラック・ブラケット(Dirac Bracket)
ブラケット記法(bra-ket notation)とは、量子力学における量子状態を記述するための標準的な記法である。2つの状態の内積がブラケットを用いて ⟨φ|ψ⟩ のように表され、この左半分 ⟨φ| をブラベクトル、右半分 |ψ⟩ をケットベクトルと呼ぶ。この記法は、英国理論物理学者ポール・エイドリアン・モーリス・ディラック(1902年8月から1984年10月)が発明したため、ディラックの記法やディラック・ブラケット(Dirac Bracket)とも呼ぶ。

(出典:DiracBracket)
Schrödinger方程式(Schrödinger equations)
シュレーディンガー方程式(Schrödinger equation)とは、物理学の量子力学における基礎方程式である。 シュレーディンガー方程式という名前は、オーストリア出身の理論物理学者であるエルヴィーン・ルードルフ・ヨーゼフ・アレクサンダー・シュレーディンガー(1887年8月から1961年1月)が1926年に波動形式の量子力学である「波動力学」に関する一連の論文を提出した。次いで量子力学の基本方程式であるシュレーディンガー方程式を発表し、1935年にはシュレーディンガーの猫を提唱した。1933年には、英国の理論物理学者ポール・ディラックと共に新形式の原子理論の発見の業績によりノーベル物理学賞を受賞している。シュレーディンガー方程式は、古典力学における「ニュートンの第二法則」を量子力学に置き換えたものである。ニュートンの第二法則は、既知の初期条件が与えられたときに、ある物理系が時間の経過とともにどのような経路をたどるかを数学的に予測するものである。シュレーディンガー方程式は、孤立した物理系の量子力学的な特徴である波動関数の時間発展を示す。シュレーディンガー方程式を用いたものを「波動力学」と呼ぶことがある。
まとめ
講義を振り返って「前提となる知識」をまず整理した。このような基本的なことを理解せずに、英文資料を英語で説明されてもとても理解がついていかない(涙)。津田教授が示された4つの論点については、次回の投稿でトライしたい。
以上
最後まで読んで頂きありがとうございました。
拝
参考:次回の構成(論点1と2、論点3と4)
論点1:ニューロンはどのように生成されたか?
論点2:機能モジュールはどのように生成されたのか?
論点3:神経細胞はどのようにして機能特異性を獲得したのか?
論点4:海馬・記憶システムの進化
今後の検討課題




