はじめに
今回は、脳型情報処理機械論の第4回講義のその3として、津田教授が提示した4つの論点の後半2つについての考察を理解した範疇でまとめてみた。
その1:4つの論点と前提となる知識 (前々回の投稿)
その2:4つの論点(前半)のレビュー (前回の投稿)
その3:4つの論点(後半)のレビュー (⇨ 今回)
4つの論点
論点1:ニューロンはどのように生成されたか?
論点2:機能モジュールはどのように生成されたのか?
論点3:神経細胞はどのようにして機能特異性を獲得したのか?
論点4:海馬・記憶システムの進化
4つの論点のポイント
論点1:ニューロンはどのように生成されたか?
ニューロンには、3つのタイプがあるとか、細胞分化したとかは理解できるが、どのように生成したかは難しい。グリア制限前駆体細胞(GRP)から生成したという説と、NEP細胞からGRPが生成し、そこからニューロンが生成された説などがあり、まだまだ未知の領域が残っているのが脳科学の魅力だと思う。詳細は前回の投稿も参照いただけるとありがたい。
論点2:機能モジュールはどのように生成されたのか?
ニューロンの結びつきは、生まれ持っての部分と生まれた後の環境に依存する部分があり、その意味ではヘテロジニアスネットワークが自然だし、興味があるものや利用する部分もどうしても偏重するのでモジュール構成になるのだろう。人工知能の場合には、基本はホモジニアスなネットワークだと言える。ただ、最近は、現場のニーズに合わせて論理回路を書き換え可能なFPGA(Field Programmable Gate Array)が注目されている。例えて言えば、日本語脳の部分や英語脳の部分などを事後的に書き換えられるのは画期的だ。つまり、リアルなコンピュータもホモジニアスなネットワークからヘテロジニアスなネットワークに進化しつつあるのではないだろうか。
論点3:神経細胞はどのようにして機能特異性を獲得したのか?
進化したリザーバーコンピュータ(Evolutionary Reservoir Computer)
リザーバーコンピュータについては、第2回講義で詳しく習った。リザーバーコンピュータは,進化的なダイナミクスを用いて内部のリザーバーを変化させることができる。これを進化的リザーバーコンピュータとも呼ばれる。入力情報に応じて特異性を示す神経細胞ユニットを開発するためには、内部ダイナミクスを制御して、拡大ダイナミクスの後に縮小ダイナミクスを生成する必要がある。膨張ダイナミクスは入力情報の違いを拡大し、収縮ダイナミクスは入力情報のクラスター形成に寄与し、複数のアトラクタを生成する。両者が同時に現れることは、カオスの存在を意味する。一方、これらのダイナミクスが有限の時間間隔で連続的に出現すると、機能分化を引き起こす可能性がある。下の図は、この進化型リザーバーコンピュータにおいて、特定のニューロンユニットがどのようにして生み出されるかを示している。
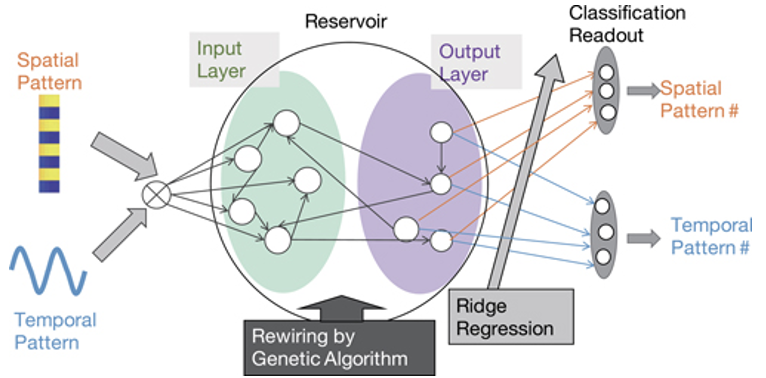
(出典:AIP)
生物学的なつながり
ニューロンは、脳の基本的な計算単位だ。人間の神経系には約860億個のニューロンが存在し、それらは約10の14乗個から10の15乗個のシナプスで接続される。下の図(左)は生物学的なニューロンのイメージ図であり、下の図(右)は、一般的な数学的モデルを示す。各ニューロンは、樹状突起から入力信号を受け取り、その単一の軸索に沿って出力信号を生成する。軸索は最終的に分岐し、シナプスを介して他のニューロンの樹状突起に接続される。ニューロンの計算モデルでは、軸索に沿って進む信号は、乗法的に相互作用する。他方のニューロンの樹状突起とそのシナプスの強度に基づいてシナプスの強度(重みw)は学習可能である。あるニューロンが他のニューロンに与える影響の強さおよびその方向を制御するという考え方である。基本的なモデルでは、樹状突起が信号を細胞体に伝え、そこですべての信号が合計される。最終的な和がある閾値を超えると、そのニューロンは発火し、軸索に沿ってスパイクを送る。計算モデルでは、スパイクの正確なタイミングは重要ではなく、発火の頻度のみが情報を伝達すると仮定する。このレートコードの解釈に基づいて、ニューロンの発火率を活性化関数fという活性化関数でニューロンの発火率をモデル化する。活性化関数としては、シグモイド関数σは入力和の信号強度を受け取る。

(出典:CS231n)
ミニマムクラシフィケーションエラー
分類誤差の最小化分類問題では、経験的リスク最小化(ERM)により学習セットの0-1分類誤差を最小化する。0-1の学習誤差をカウントする目的関数の構築方法を考える。分類規則を用いると、任意の線形モデルが与えられた場合、トレーニングセット内の各トレーニングサンプルについて、それが誤分類エラーにつながる問題を解決するための一般的なトリックは、ステップ関数を近似するために滑らかな関数を使用することである。よく知られているのがシグモイド関数(ロジスティックシグモイド)だ。シグモイド関数はどこでも微分可能であり、その傾きが十分に大きい限りステップ関数を近似できる。
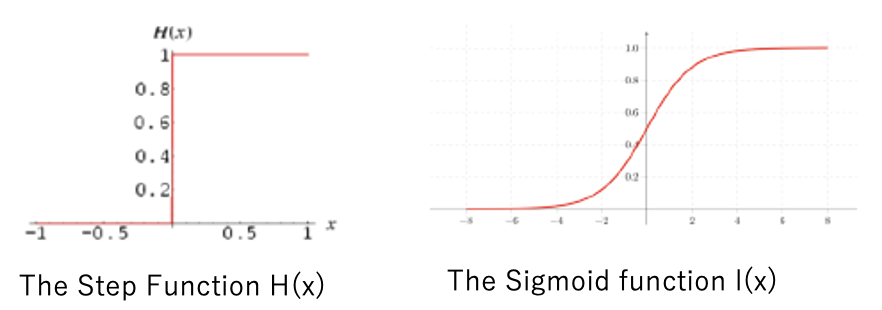
(出典:cheg)
スイッチングシナプス(Switching Synapse)
人間の脳は複雑に統合された時空間システムである。どのニューロンが発火したかと言う空間の問題と、ニューロンが発火したときの時間の問題の両方が認知機能で処理される。このため、脳のエネルギー効率と演算機能を両立させるには、空間と時間の両方の領域で動作する方法論が必要だ。シナプス可塑性を持つナノスケールのデバイスに時空間機能を実装することは、人間の脳の演算性能とエネルギー性能をエミュレートする大規模なニューロモーフィックシステムの構築に向けた大きな一歩となる。抵抗性スイッチングシナプスを用いて、脳のような時空間コンピューティングを実現するためのニューロモーフィックなアプローチが提案されている。時空間のスパイクパターンを処理するために、時間コード化されたスパイクは指数関数的に減衰する信号に再形成され、McCulloch-Pittsニューロンに供給される。MacCullochとPittsは、ニューロンが論理的な制御素子であると仮定し、そのモデルでは「and」「or」「not」といった基本的な論理演算が可能であり、さらに複雑な結合モデルを構築できると提案した。提案されたニューラルネットワークモデルにおいて、ニューロンへの入力は、そのニューロンに接続する他のニューロンからの出力に結合重みを乗じたものの総和で表される。抵抗性スイッチングシナプスを持つ複数のニューロンネットワークを教師付きで学習させたところ、スパイクシーケンスの認識が実証された。最後に、正確なスパイクのタイミングに対する感度により、時空間ニューラルネットワークが人間の脳の音の方位検出を模倣することができる。
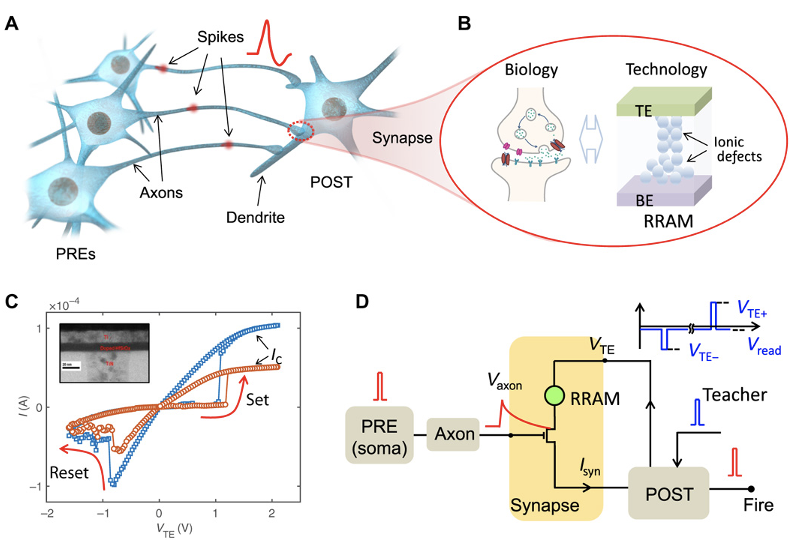
(出典:Science)
アトラクター(Attractor)
力学系におけるアトラクター(attractor)とは、時間発展する軌道を引き付ける性質を持った相空間上の領域である。力学系において重要なトピックの一つ。引き込まれた後の軌道は、アトラクター内に留まり続ける。アトラクターへ引き込まれる初期値の集合はベイスンや吸引領域と呼ばれる。アトラクターは、その構造・性質にもとづき点アトラクター、周期アトラクター、準周期アトラクター、ストレンジアトラクターの4種類に分類される。点アトラクターはもっとも単純で、周りの軌道を引き寄せる1つの点である。周期アトラクターと準周期アトラクターは、連続力学系でいえばそれぞれ閉曲線とトーラスの形を成す。ストレンジアトラクターは、カオスと呼ばれる非周期的軌道から成るアトラクターで、バタフライ効果として知られる初期値鋭敏性とフラクタルな幾何学的構造を持つ。下の図(左)は連続時間力学系のファン・デル・ポール方程式で現れる周期アトラクターである。軌道は各矢印に沿って赤い閉曲線へ引き込まれる。下の図(中)は離散時間力学系のグモウスキー・ミラの写像で現れるストレンジアトラクターだ。赤い軌道が複雑な黒点の連なりの領域へ引き込まれる。下の図(右)はエノン写像に一見類似の離散力学系で現れる準周期アトラクターだ。赤と青の軌道は黒点が連なってできる準周期軌道に引き込まれる。物理的なアトラクターの典型的な例は、減衰や摩擦を受けて振動しながら最終的に静止する振り子で、これは点アトラクターの一種である。実現象で起こるアトラクターを限られた時系列データから再現する手法はアトラクターの再構成として知られ、実現象の力学系的性質の調査や、実物の品物に対する異常検出といった応用研究にも用いられる。
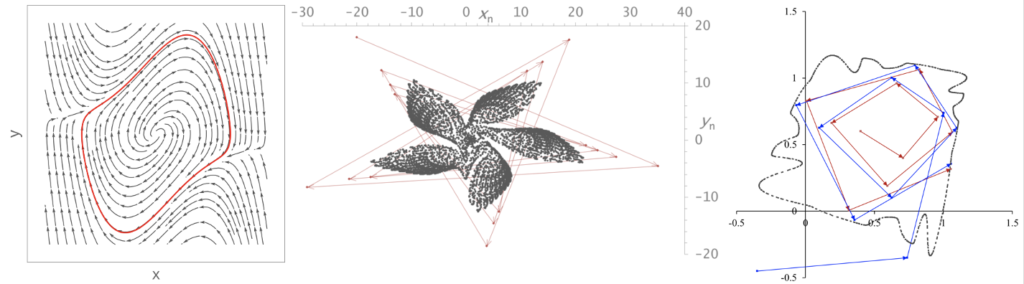
(出典:アトラクター)
DYNAPOLプロジェクト
DYNAPOLは、様々な技術的用途のための新しいタイプの人工材料を設計するための新しいルートを探り、異なる革新的な化学的・物理的コンセプトの材料を使用し、自己組織化の特性を活用する。温度、塩分濃度、圧力等の環境や、タンパク質や組織との特定の相互作用等の生物学的要因などの外部刺激に積極的に反応する。天然の超分子材料の例としては、微小管やタンパク質のフィラメントがあり、これらは特定の入力に応じて再構成することができる。DYNAPOLプロジェクトは、マルチスケールの分子モデルを開発し、高度な計算シミュレーションと機械学習技術を用いて、生体にヒントを得たダイナミックな特性を持つ、あるいは生体と同様の特性を持つ新しいクラスの人工材料を設計する方法を学ぶための基本的な化学的・物理的原理を発見することを狙いとしている。バイオインスパイアされた人工高分子材料を設計するためには、その動的挙動を制御する分子原理を理解し、構成的な自己組織化ビルディングブロックの化学構造と、それらが様々な時空間スケールで形成する集合体の動的特性との間に存在する関係を知ることが必要である。この目的のために、DYNAPOLプロジェクトでは、マルチスケールの分子モデル、高度な分子シミュレーション技術、機械学習を用いる。
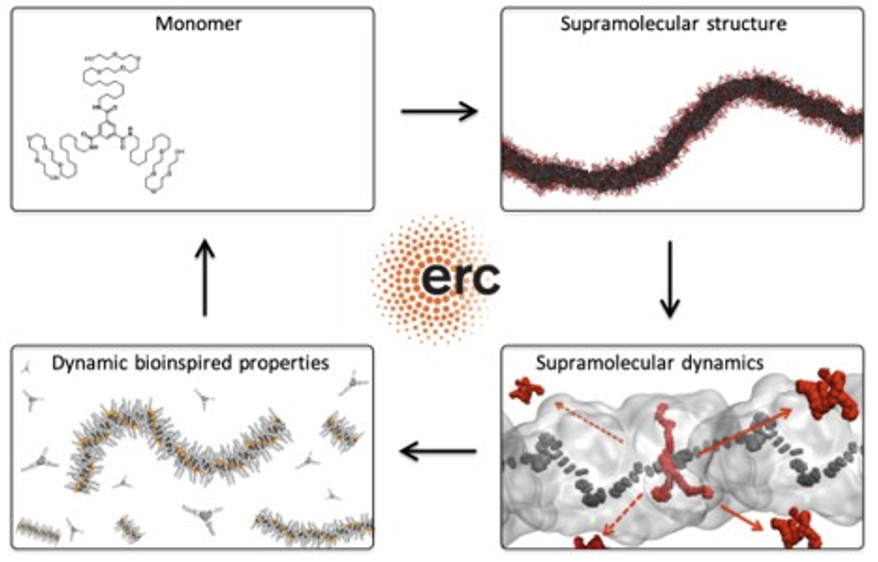
(出典:ERC)
論点4:海馬・記憶システムの進化
海馬の安定した記憶エングラムと動的な記憶エングラム(Parallel emergence of stable and dynamic memory engrams in the hippocampus)
私たちの日常生活の中での記憶は、特定の神経細胞群、すなわち「エングラム」の活動によって表現される。ニューロンエングラムは、学習中にシナプスの変化によって組み立てられ、エングラムの再活性化が記憶された経験を表す。意識的な記憶のエングラムでは、まず海馬に数日間保存された後、大脳皮質領域に移される。海馬の歯状回では、顆粒細胞が内嗅皮質からの豊富な入力をまばらな出力に変換し、海馬領域CAの高度に相互接続された錐体細胞ネットワークに転送される。CA3の錐体細胞は、海馬の出力領域であるCA1に投射する。海馬では一過性の記憶が保存されている。CA1とCA2のエングラムは時間が経つと安定しないが、歯状回のエングラムが再活性化すると数週間経っても人工的な記憶の想起が可能だ。このパラドックスを解決するには、学習中の歯状回顆粒細胞からの記録が必要であるが、1日以上の記録はない。頭部を固定したマウスを用いて、仮想環境下で複数日にわたる空間記憶課題を実施し、慢性的な2光子カルシウムイメージングを行い、海馬の主要な下位野すべてのニューロン活動を記録する実験が行われた。この結果によると、CA1-CA3の錐体細胞は、行動パラダイムにおいて、学習した空間シーンを正確かつ高度に文脈特異的に表現する。歯状回の顆粒細胞は、何日も安定した空間コードを持つことが発見された。つまり、海馬の3つのシナプスループに沿ったシナプスの重みは、歯状回から提供された安定したコードに基づいて、下流の海馬領域における動的な表現の形成をサポートするために、常に再配置されていると考えられる。
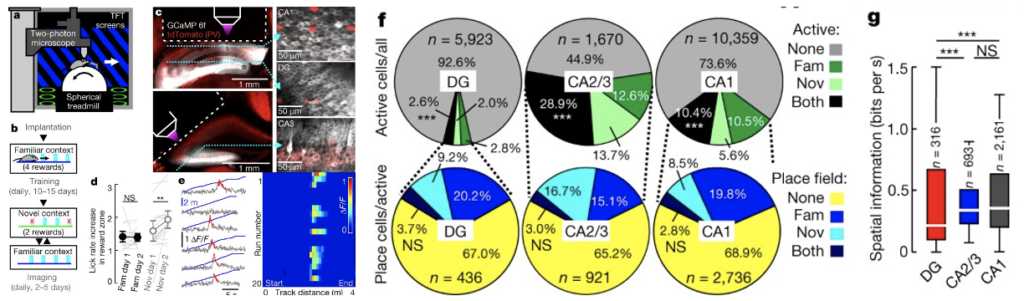
(出典:nature)
海馬(hippocampus)の機能構成
海馬(hippocampus)の機能的構成は、その長手方向に沿った勾配として分布しており、多様な脳システムとの相互作用の違いを説明している。成人の海馬の縦軸に沿って抽出したヒト組織サンプルの位置を100個以下の遺伝子の発現パターンを用いて2mm以内で予測できた。この特定の遺伝子の発現パターンの変化を脳全体で調べたところ、前・腹・後の明確な勾配が見られた。その結果、社会的行動や動機づけに関与し、前海馬と機能的に結合している前頭葉および前側頭葉領域と、視空間認知に関与し、後海馬と機能的に結合している後頭頂後頭領域は、明確に区別されることがわかった。これらの結果から、ヒトの海馬は、1つの分子勾配によって規定された2つの主要な脳システムの境界に位置していることと言える。
aの上:海馬の体積の重心に沿って、ボクセルの湾曲した骨格を取り付けた。
aの中:組織サンプル(オレンジ色)は、最も近いスケルトンボクセル(青色)に合わせた。
aの下:縦軸のサンプルの位置は、サンプルにマッチしたスケルトンボクセルのY軸座標として表された。
b:10回のクロスバリデーションを行った10種類のLASSO-PCRモデルで予測されたサンプル位置。
c:海馬表面のレンダリングでは、各頂点がその頂点に最も近いサンプルの予測位置を示している。
d:leave-one-subfield-outモデルのサンプル位置の予測値と観察値の比較。
e:leave-one-donor-outモデルにおけるサンプル位置の予測値と観測値の比較。
f:LASSO-PCRモデルにおいて最も重要な100個のプローブを反復的に除去し、各除去後に長手方向に沿ったサンプル位置を予測する10倍クロスバリデーションの精度を記録した(青点)。
g:パネルFから100本のプローブを除去した最初の50ラウンド。100本、600本、2700本の遺伝子を除去した後に変曲点が確認された。
h:パネルGの変曲点で特定された異なる遺伝子セット(青)、100個のランダムなセット内プローブのサンプル(緑)、およびランダムなプローブのサンプル(オレンジ)を入力として使用した。
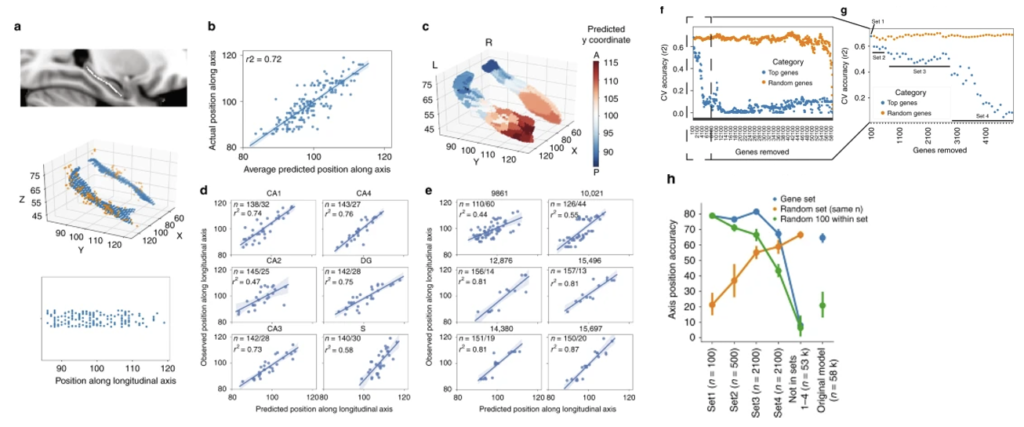
(出典:nature)
ダイナミックシステムとしてのフレキシブルモータのタイミング(A Dynamical Systems Perspective on Flexible Motor Timing)
柔軟な運動タイミングをとるには、神経活動が状態空間を通過する速度を制御する必要がある。大脳皮質のニューロンネットワークへの入力や初期条件を設定することで、行動に関連する複数の計算を選択する手段が得られるかもしれない。力学系の視点は、さまざまな感覚運動行動における時間的柔軟性の計算原理を理解するための統一的な枠組みを提供する。高次脳機能の特徴は、内的・外的な手がかりに基づいて行動反応を迅速かつ柔軟に調整する能力である。動的システムの観点から、入力や初期条件を操作することで、このようなシステムの時間的な柔軟性をどのように実現できるか。運動の時間的制御や、学習、シーケンス生成の領域に関連する未解決の問題に対処するための一般的な枠組みとして、動的システムの視点の広範な有用性と限界が研究されている。

(出典:Science that inspires)
ニューロンの動的相互結合モデル
固定されたヒトの解剖学的コネクトームで実行されるニューロンの動的システムが、長期的な可塑性では説明できない。ヒトの脳機能に関連する機能レパートリーの豊かな変化をどのようにして生み出すことができるのかは明らかではない。神経調節は、固定された解剖学的コネクトームの効果を動的に更新することで柔軟性を可能にするように進化した。神経細胞と神経伝達系の動的な相互結合をモデル化した理論的枠組みが模索されている。拡散MRI、機能的磁気共鳴画像(fMRI)、陽電子断層撮影(PET)などのマルチモーダルなニューロイメージングデータを用いて健常者におけるシロシビンによる特定のセロトニン受容体刺激の機能的効果が説明される。シロシビンがうつ病、不安障害、依存症などの神経精神疾患の治療薬として有望視されている。脳の機能を理解するためには、神経細胞と神経伝達系の相互作用が不可欠である。
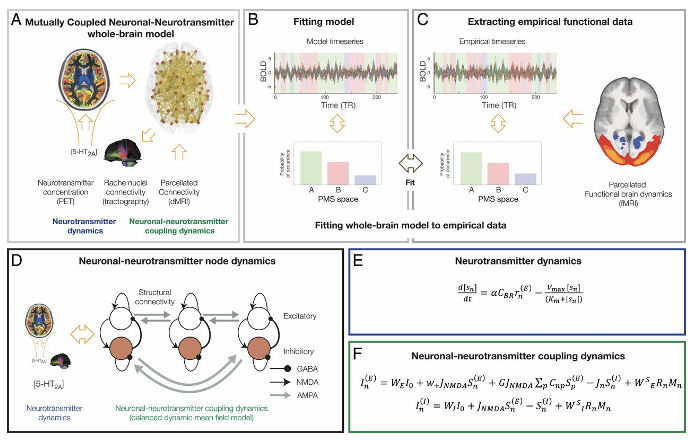
(出典:pnas)
今後の検討課題
数学的アプローチ
連続増加関数h:[0,1] → [0,1]
連続関数:R → R
連続関数:[0,1]^ → R
実数値の(j=1,2,⋯,),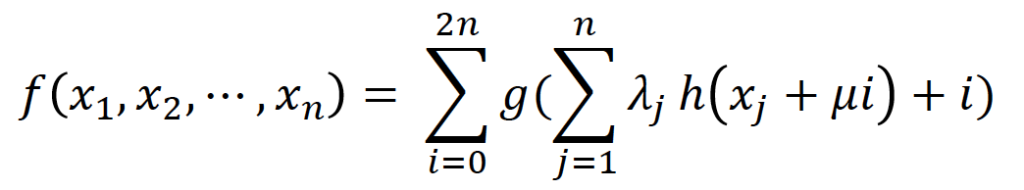
まとめ
第4回講義を受けながら、意味不明な言葉や考え方がいっぱい出てきて、その一部については、理解できたけど、まだまだ理解が不十分だ。講師が配布した資料を勝手にWEBに掲載するわけにもいかず、今回は少し(だいぶ)消化不良のままの投稿となったことをご容赦いただきたい。ただ、今まで漠然と脳科学とか、ニューロンという言葉を耳にしていたが、その詳しいメカニズムがかなり精緻に解析されつつあることを理解できたことは喜びだ。さらには津田教授のようにそれを数式で表そうという試みもなされている。これからもこの分野については、引き続きアンテナを張って情報をアップデートしていきたいと思った。
以上
最後まで読んで頂きありがとうございました。
拝




